
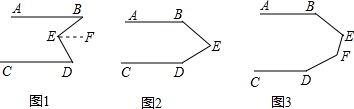
分析 (1)先根据平行线的性质得出∠B=∠BEF,由AB∥CD,EF∥AB可知EF∥CD,故∴∠D=∠FED,由此可得出结论;
(2)过点E引一条直线EF∥AB,根据EF∥AB可知∠B+∠BEF=180°,由AB∥CD,EF∥AB得出EF∥CD,故∠FED+∠D=180°,由此可得出结论;
(3)分别过点EF作EG∥AB,HF∥CD,则∠B+∠BEG=180°,∠D+∠HFD=180°,根据AB∥CD,EG∥AB,HF∥CD可知EG∥HF,故∠GEF+∠HFE=180°,由此可得出结论.
解答 解:(1)过点E引一条直线EF∥AB,
∵EF∥AB,
∴∠B=∠BEF(两直线平行,内错角相等),
∵AB∥CD,EF∥AB,
∴EF∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
∴∠D=∠FED(两直线平行,内错角相等).
故答案为:两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠FED;两直线平行,内错角相等.
(2)如图2,过点E引一条直线EF∥AB,
∵EF∥AB,
∴∠B+∠BEF=180°.
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠FED+∠D=180°,
∴∠B+∠BEF+∠FED+∠D=180°+180°=360°,即∠B+∠BED+∠D=360°
(3)如图3,分别过点EF作EG∥AB,HF∥CD,
∵EG∥AB,
∴∠B+∠BEG=180°.
∵HF∥CD,
∴∠D+∠HFD=180°.
∵AB∥CD,EG∥AB,HF∥CD,
∴EG∥HF,
∴∠GEF+∠HFE=180°,
∴∠B+∠BEF+∠EFD+∠D=540°.
故答案为:540°.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
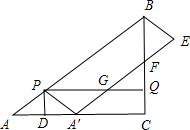 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,4) | B. | (-4,3) | C. | (3,-4) | D. | (4,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 100 | 200 | 400 | 1000 | … |
| y(元) | 40 | 80 | 160 | 400 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )| A. | 16 | B. | 8 | C. | 8$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 学生 | 作业 | 测验 | 期中考试 | 期末考试 |
| 小丽 | 80 | 75 | 71 | 88 |
| 小明 | 76 | 80 | 68 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
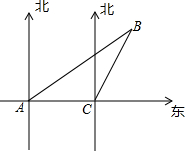 三个小岛A、B、C的位置如图所示,在A处测得小岛B在A的北偏东52°方向,在C处测得小岛B在C的北偏东26°方向,且A、B之间的距离是1000海里,求:小岛C在小岛A的正东方向多少海里?(精确到1海里)
三个小岛A、B、C的位置如图所示,在A处测得小岛B在A的北偏东52°方向,在C处测得小岛B在C的北偏东26°方向,且A、B之间的距离是1000海里,求:小岛C在小岛A的正东方向多少海里?(精确到1海里)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com