练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．当a≠-$\frac{1}{3}$时，关于x的方程（3a+1）x2+5ax+4=0是一元二次方程．

    分析 根据一元二次方程的定义得到3a+1≠0，由此求得a的取值范围．

    解答 解：∵关于x的方程（3a+1）x2+5ax+4=0是一元二次方程，
    ∴3a+1≠0，
    解得a≠-$\frac{1}{3}$．
    故答案是：≠-$\frac{1}{3}$．

    点评 本题利用了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2+bx+c=0（且a≠0）．特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

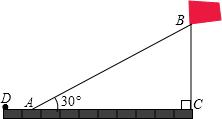    8．如图，小明利用升旗用的绳子测量学校旗杆BC的高度，当绳子从旗杆端垂下，地上部分还有8米，若把绳子往外拉直，绳子末端接触地面A点并与地面形成30°角，求旗杆BC的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．用●表示实心圆，用○表示空心圆，现有若干个实心圆与空心圆，按一定的规律排列如下：●○●●○●●●○●○●●○●●●○●○●●○●●●○…问：前2016个圆中，有672个空心圆．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（1）计算（-1）2010-|-7|+$\sqrt{9}$×（$\sqrt{5}$-π）0+$\root{3}{27}$
    （2）求x的值：
    ①3（x+1）2-75=0．
    ②2（x-1）3+16=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点画图形．
    （1）在图①中，画一个面积为8的正方形；
    （2）在图②，画一个直角三角形，使它们的三边长都是无理数．
    （3）图③中，画一个三角形，使它是轴对称图形，并且面积最大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

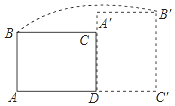    3．如图，在矩形ABCD中，AB=3，AD=4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′，则点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是多少？（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．写出一个抛物线开口向下，与y轴交于（0，2）点的函数表达式y=-x2+x+2（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．计算结果不可能m8的是（　　）
    A．m4•m4B．（m4）2C．（m2）4D．m4+m4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．无论x取何值，总是有意义的分式是（　　）
    A．$\frac{x}{2x+1}$B．$\frac{2x}{{x}^{2}+1}$C．$\frac{3x}{{x}^{3}+1}$D．$\frac{x+1}{{x}^{2}}$

    查看答案和解析>>

    同步练习册答案