
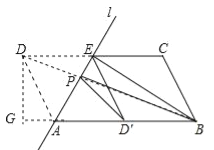
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG=![]() ,DG=
,DG=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
试题解析:(1)证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴CE=D′B,CE∥D′B,
∴四边形BCED′是平行四边形;
∵AD=AD′,
∴DAD′E是菱形,
(2)∵四边形DAD′E是菱形,
∴D与D′关于AE对称,
连接BD交AE于P,则BD的长即为PD′+PB的最小值,
过D作DG⊥BA于G,
∵CD∥AB,
∴∠DAG=∠CDA=60°,
∵AD=1,
∴AG=![]() ,DG=
,DG=![]() ,
,
∴BG=![]() ,
,
∴BD=![]() =
=![]() ,
,
∴PD′+PB的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】遂宁市明星水利为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
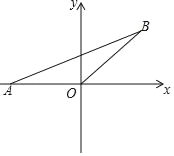
【题目】如图,等腰△AOB中,AO=BO=2,点A在x轴上,OB与x轴的夹角为45°;
(1)求直线AB、OB的解析式;
(2)若将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.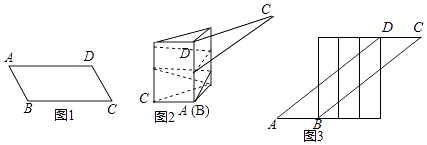
(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,分别把两个边长为![]() 的小正方形沿一条对角线裁成
的小正方形沿一条对角线裁成![]() 个小三角形拼成一个大正方形,则大正方形的边长为_______
个小三角形拼成一个大正方形,则大正方形的边长为_______![]() ;
;

(2)若一个圆的面积与一个正方形的面积都是![]() ,设圆的周长为
,设圆的周长为![]() ,正方形的周长为
,正方形的周长为![]() ,则
,则![]() _____
_____![]() (填“
(填“![]() ”或“
”或“![]() ”或“
”或“![]() ”号);
”号);
(3)如图,若正方形的面积为![]() ,李明同学想沿这块正方形边的方向裁出一块面积为
,李明同学想沿这块正方形边的方向裁出一块面积为![]() 的长方形纸片,使它的长和宽之比为
的长方形纸片,使它的长和宽之比为![]() ,他能裁出吗?请说明理由?
,他能裁出吗?请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
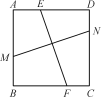
【题目】如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF.你认为( )
A. 仅小明对 B. 仅小亮对 C. 两人都对 D. 两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1= ![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a= ![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2.其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2.其中正确结论的个数是( )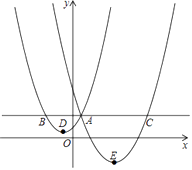
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知两点A(3,m),B(2m,4),且A和B到x轴距离相等,求B点坐标.
(2)点A在第四象限,当m为何值时,点A(m+2,3m5)到x轴的距离是它到y轴距离的一半.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=﹣ ![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com