
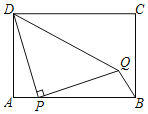
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点(不与
边上任意一点(不与![]() 点重合),连接
点重合),连接![]() ,以线段
,以线段![]() 为直角边作等腰直角
为直角边作等腰直角![]() (点
(点![]() 在直线
在直线![]() 右侧),
右侧),![]() ,连接
,连接![]() ,则
,则![]() 的最小值为_____.
的最小值为_____.
【答案】![]()
【解析】
过Q作QE⊥AB于E,在EP上截取EF=EQ,连接QF,根据全等三角形性质得出AF=PE=10,依据△EFQ是等腰直角三角形可得FQ与FB夹角始终为45°,进而得到当BQ⊥FQ时,BQ最小,根据△BQF为等腰直角三角形进一步求解即可得出BQ长度.
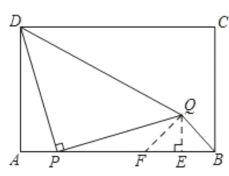
如图所示,过Q作QE⊥AB于E,在EP上截取EF=EQ,连接QF,
∵△DPQ为等腰直角三角形,四边形ABCD为矩形,
∴DP=PQ,∠A=∠PEQ,
易证:∠ADP=∠EPQ,
∴△ADP≌△EPQ(AAS),
∴AP=QE=EF,AD=PE=10,
∴AF=PE=10,
∵△EFQ为等腰直角三角形,
∴∠QFE=45°,即FQ与FB夹角始终为45°,
∴如图所示,当BQ⊥FQ时,BQ最小,此时△BQF为等腰直角三角形,
又∵QE⊥BF,
∴BE=EF=QE=AP,
∵PE=10,
∴BE=AP=![]() ,
,
∴BF=5,
∴BQ=cos45°BF=![]()
即BQ最小值为![]()
故答案为:![]()


科目:初中数学 来源: 题型:
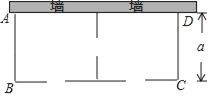
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
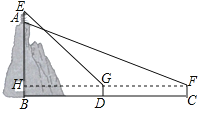
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
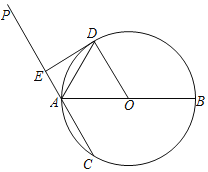
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以O为圆心,OB为半径作圆,过C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)已知AC=6,求扇形OBC围成的圆锥的底面圆半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.

(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
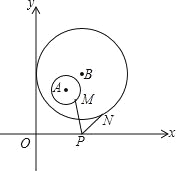
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
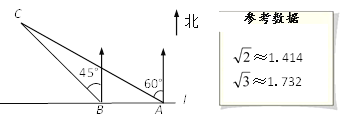
【题目】如图,同学们利用所学知识去测量海平面上一个浮标到海岸线的距离. 在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,小宇同学在A处观测得浮标在北偏西60°的方向,小英同学在距点A处60米远的B点测得浮标在北偏西45°的方向,求浮标C到海岸线l的距离(结果精确到0.01 m).
查看答案和解析>>
科目:初中数学 来源: 题型:
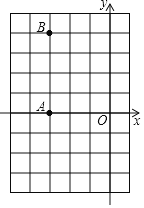
【题目】坐标为整数的点叫格点,如图,已知A(-3,0)、B(-3,4)和原点都是格点,在如图6×9的网格中使用无刻度的直尺按要求作图.
(1)找格点C,连BC,使BC与OA的交点就是OA的中点,画出图形直接写出C点坐标.
(2)按以下方法可以作出∠AOB的平分线.
第一步:找格点D,使OD=OB;
第二步:找格点E,使DE⊥OB交AB于F;
第三步:连OF,则OF是∠AOB的平分线;
请你按步骤完成作图,并写出D、E三点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com