
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
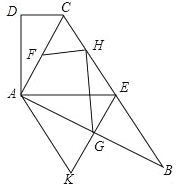
(1)求证:AC2=CD·BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
【答案】(1)证明过程见解析;(2)证明过程见解析.
【解析】
(1)欲证明AC2=CDBC,只需推知△ACD∽△BCA即可;(2)①连接AH.构建直角△AHC,利用直角三角形斜边上的中线等于斜边的一半、等腰对等角以及等量代换得到:∠FHG=∠CAB=90°,即FH⊥GH;
②利用“在直角三角形中,30度角所对的直角边等于斜边的一半”、“直角三角形斜边上的中线等于斜边的一半”推知四边形AKEC的四条边都相等,则四边形AKEC是菱形.
解:(1)∵AC平分∠BCD,∴∠DCA=∠ACB.
又∵AC⊥AB,AD⊥AE,
∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.
又∵E是BC的中点, ∴AE=BE,
∴∠EAB=∠ABC,∴∠DAC=∠ABC,
∴△ACD∽△BCA,∴![]() ,
,
∴![]() =CD·BC;
=CD·BC;
(2)①证明:连接AH.∵∠ADC=∠BAC=90°,点H、D关于AC对称,∴AH⊥BC.
∵EG⊥AB,AE=BE,
∴点G是AB的中点,
∴HG=AG,∴∠GAH=∠GHA.
∵点F为AC的中点,
∴AF=FH,∴∠HAF=∠FHA,
∴∠FHG=∠AHF+∠AHG=∠FAH+∠HAG=∠CAB=90°,
∴FH⊥GH;
②∵EK⊥AB,AC⊥AB, ∴EK∥AC,
又∵∠B=30°,∴AC=![]() BC=EB=EC.
BC=EB=EC.
又EK=EB,∴EK=AC,
即AK=KE=EC=CA,∴四边形AKEC是菱形.
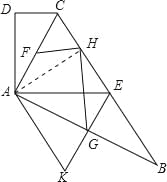


科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,1辆大货车与3辆小货车额定载重量的总和为23吨,2辆大货车与5辆小货车额定载重量的总和为41吨. 1辆大货车、1辆小货车的额定载重量分别为多少吨?设1辆大货车的额定载重量为x吨,1辆小货车的额定载重量为y吨,依题意,可以列方程组为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何大于1的正整数m的三次幂均可分裂成m个连续奇数的和。如:23=3+5、33=7+9+11、43=13+15+17+19……依此规律,若m3分裂后其中有一个奇数是2019,则m的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加射击比赛,10次射击的成绩如表:
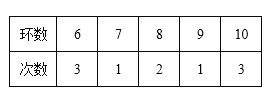
若小明再射击2次,分别命中7环、9环,与前10次相比,小明12次射击的成绩( )
A. 平均数变大,方差不变B. 平均数不变,方差不变
C. 平均数不变,方差变大D. 平均数不变,方差变小
查看答案和解析>>
科目:初中数学 来源: 题型:
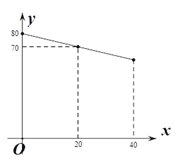
【题目】某果农的苹果园有苹果树60棵,由于提高了管理水平,可以通过补种一些苹果树的方法来提高总产量.但如果多种树,那么树之间的距离和每棵树所受的光照就会减少,单棵树的产量也随之降低.已知在一定范围内,该果园每棵果树产果y(千克)与补种果树x(棵)之间的函数关系如图所示.若超过这个范围,则会严重影响果树的产量.
(1)求y与x之间的函数关系式;
(2)在这个范围内,当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
(3)若该果农的苹果以3元/千克的价格售出,不计其他成本,按(2)的方式可以多收入多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为圆O上一点,点C在直径AB的延长线上,且∠CAD=∠BDC,过点A作⊙O的切线,交CD的延长线于点E.
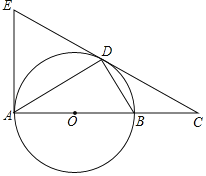
(1)求证:CD是⊙O的切线;(2)若CB=3,CD=9,求ED的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com