
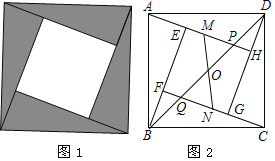
����Ŀ���ҹ��Ŵ���ѧ����ˬ������ͼ֤���˹��ɶ�����������������ˬ��ͼ����ͼ1�����������ĸ�ȫ�ȵ�ֱ��������ƴ�����ڡ��ⶼ�������ε�����ͼ��������ͼ�У���ͼ2������֪��OΪ������ABCD�ĶԽ���BD���е㣬�Խ���BD�ֱ�AH��CF�ڵ�P��Q����������EFGH��EH��FG�����Ϸֱ�ȡ��M��N����MN������O����MH��3ME��BD��2MN��4![]() �����APD�����Ϊ_____��
�����APD�����Ϊ_____��
���𰸡�5
��������
����FH����EK��MN��OL��DG��ͨ�������ε����ʺ�ȫ�������ε������Լ����ɶ�������EM��1���ɵ�EH��4���ɹ��ɶ�������HD��2��AH��6����ƽ���ߵ����ʿɵ�PH��1��������⣮
��ͼ������FH����EK��MN��OL��DG
���ı���ABCD�������Σ���BD��2MN��4![]()
��MN��2![]() ��AB��2
��AB��2![]()
���ı���EFGH��������
��FO��HO��EH��FG
���HMO����FNO����MHO����NFO����FO��HO
���MHO�ա�FNO��AAS��
��MH��FN
��MH��3ME��
��MH��FN��3EM��EH��EF��4EM
��EK��KN��EH��FG
���ı���EMNK��ƽ���ı���
��MN��EK��2![]() ��KN��EM
��KN��EM
��FK��2EM
��EF2+FK2��EK2��
��16EM2+4EM2��20
��EM��1
��EH��4��
��AD2����AE+4��2+DH2����AE��DH
��DH��AE��2
��AH��6
��PH��OL
��![]()
��PH��1
��AP��5
��S��APD��![]() ��5��2��5
��5��2��5
�ʴ�Ϊ��5.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
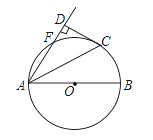
����Ŀ����ͼ��AB����O��ֱ������F��C����O����![]() �� ����AC��AF������C��CD��AF��AF���ӳ����ڵ�D��
�� ����AC��AF������C��CD��AF��AF���ӳ����ڵ�D��
��1����֤��CD����O�����ߣ�
��2����![]() �� CD=4������O�İ뾶��
�� CD=4������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
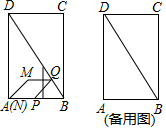
����Ŀ����ͼ���ھ���ABCD�У�AB=2cm����ADB=30�㣮P��Q����ֱ��A��Bͬʱ��������P������AB��BC�˶�����AB�ϵ��ٶ���2cm/s����BC�ϵ��ٶ���2![]() cm/s����Q��BD����2cm/s���ٶ����յ�D�˶�������P��PN��AD������Ϊ��N������PQ����PQ��PNΪ�ڱ���PQMN�����˶���ʱ��Ϊx��s����PQMN�����ABCD�ص����ֵ�ͼ�����Ϊy��cm2��
cm/s����Q��BD����2cm/s���ٶ����յ�D�˶�������P��PN��AD������Ϊ��N������PQ����PQ��PNΪ�ڱ���PQMN�����˶���ʱ��Ϊx��s����PQMN�����ABCD�ص����ֵ�ͼ�����Ϊy��cm2��
��1����PQ��ABʱ��x���ڶ��٣�
��2����y����x�ĺ�������ʽ����д��x��ȡֵ��Χ��
��3��ֱ��AM������ABCD������ֳ�1��3������ʱ��ֱ��д��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������֯�༶�����ᣬ������齱���ڣ�ÿ��ͬѧ����һ�γ齱���ᣬ�齱�������£���һ���˿����е���Ϊ��2������3������3������5������6���������Ʊ��泯��ϴ�ȣ��ȴ��г��1���ƣ��ٴ����µ�4�����г��1���ƣ���¼�����Ƶ�����Żأ����һ�γ齱����ÿ�γ�������Ƶ���֮��Ϊ![]() ��������Ҫ��ȷ�����
��������Ҫ��ȷ�����

��1�����б�����״ͼ�ķ��������ͬѧ���һ�Ƚ��ĸ��ʣ�
��2���Ƿ�ÿ�γ齱�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�������˸��ţ����ǣ��������£�ij��ѧΪ����ѧ����Ұ����չ������ѧ��ѧ�������������˾��꼶����ѧ��һ�ܵĿ���ѧϰ��ѧʱ�䣬����������Ƴ�������������ͳ��ͼ���������ͳ��ͼ����Ϣ�ش��������⣺
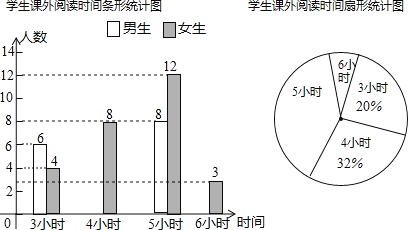
��1�����ε����ѧ������Ϊ____________�ˣ�������ѧ������ѧϰ��ѧʱ�����λ����____________Сʱ��������������������Сʱ��
��2�����㲹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�����ѧϰ��ѧʱ��Ϊ5Сʱ�����ε�Բ�ĽǶ�����____________��
��4�����꼶��ѧ��700�ˣ����ƾ��꼶һ�ܿ���ѧϰ��ѧʱ�䲻����5СʱСʱ��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1������![]() Ϊ
Ϊ![]() �е�ʱ����
�е�ʱ����![]() ��
��![]() ����ֱ��д���𰸣�
����ֱ��д���𰸣�
��2���������˶������У�![]() ��ֵ�Ƿ��仯�������䣬�������ֵ�����仯����˵�����ɣ�
��ֵ�Ƿ��仯�������䣬�������ֵ�����仯����˵�����ɣ�
��3����![]() Ϊ����������ʱ���������������������
Ϊ����������ʱ���������������������![]() �ij��ȣ�
�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶ѧ����ѧ��ĩ���������С�������ȡ�˲���ѧ������ѧ�ɼ�(������Ϊ����)Ϊ��������ΪA��![]() �֣�B��
�֣�B��![]() �֣�C��
�֣�C��![]() �֣�D��
�֣�D��![]() ���ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ���Ƴ����������в�������ͳ��ͼ�������ͼ����Ϣ����������⣺
���ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ���Ƴ����������в�������ͳ��ͼ�������ͼ����Ϣ����������⣺
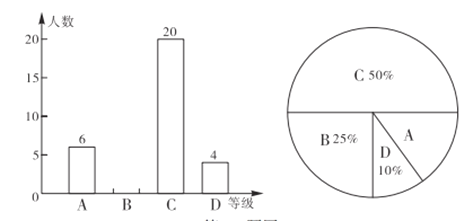
��1����������ȡ��ѧ�����ж����ˣ�
��2���뽫����ͳ��ͼ����������
��3����У���꼶����ѧ��![]() �ˣ�������Ϊ
�ˣ�������Ϊ![]() ������(��
������(��![]() ��)Ϊ�����������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��Լ�ж����ˣ�
��)Ϊ�����������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
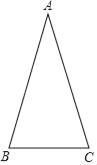
����Ŀ����ͼ������ABC�У�AB=AC����D��AB���ϣ���D����A�ľ������D����C�ľ�����ȣ�
��1�����ó߹���ͼ������D����д������������ͼ�ۼ���
��2������ABC�ĵױ߳�5���ܳ�Ϊ21������BCD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ�(2��0)��(3��0)֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0���ܵ���1��x��3ʱ��y��0��������ȷ���ǣ� ��
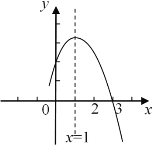
A.�٢�B.�٢ڢ�C.�ڢۢ�D.�ۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com