
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的一点,且
的一点,且![]() ,
,![]() 是
是![]() 上一点,射线
上一点,射线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)当点![]() 为
为![]() 中点时,则
中点时,则![]() ,
,![]() ;(直接写出答案)
;(直接写出答案)
(2)在整个运动过程中,![]() 的值是否会变化,若不变,求出它的值;若变化,请说明理由;
的值是否会变化,若不变,求出它的值;若变化,请说明理由;
(3)若![]() 为等腰三角形时,请求出所有满足条件的
为等腰三角形时,请求出所有满足条件的![]() 的长度.
的长度.

【答案】(1)8,![]() ;(2)不变,
;(2)不变,![]() ;(3)
;(3)![]() 或1或
或1或![]()
【解析】
如图1,过G作GH⊥AD于H,先证明AE=AM=2,得∠AEM=∠DEF=45°,则DF=DE=8,再求CG的长,根据勾股定理计算EG的长;
(2)根据ME⊥EG,证明△AME∽△HEG,△EHG∽△FDE,可得![]() ,可得∠EGM=∠EFG.可得∠MGF=90°,由三角函数定义可得结论;
,可得∠EGM=∠EFG.可得∠MGF=90°,由三角函数定义可得结论;
(3)设AM=m,则BM=4-m,DF=4m,证明△MBG∽△GCF,表示CG=8-2m,BG=2+2m.分三种情况进行讨论,根据平行线分线段成比例定理和三角函数定义列等式可得结论.
(1)如图1,过G作GH⊥AD于H,
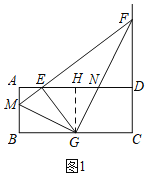
∵点M为AB中点,AB=4,
∴AM=2,
∵AE=2,
∴AE=AM=2,
∴DE=10-2=8,
∵四边形ABCD是矩形,
∴∠A=∠CDA=90°,
∴∠AEM=∠DEF=45°,
∴DF=DE=8,
∵EG⊥ME,
∴∠MEG=90°,
∴∠HEG=∠EGH=45°,
∴GH=EH=4,
∴![]() ,
,
故答案为: 8,![]()
(2)∵![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,
∴∠EGM=∠EFG.
∴∠EGM=∠EFG.
∵∠EGF+∠EFG=90°,
∴∠EGF+∠EGM=90°,即∠MGF=90°,
∴![]() .
.
(3)设![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
(ⅰ)当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,
,
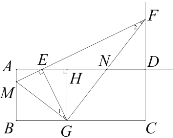
则![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]()
解得![]() 或
或![]() (舍去).
(舍去).
(ⅱ)当![]() 是,
是,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
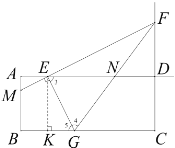
∴![]() ,
,
∴![]() .
.
(ⅲ)当![]() 时,
时,![]() .
.
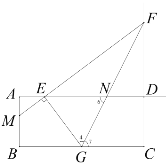
∵![]() ,∴
,∴![]() ,
,
∴![]()
∴![]()
∴![]() .
.
综上所述:当![]() 或1或
或1或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】在抗疫期间,药店销售![]() 两种类型的口罩,已知销售
两种类型的口罩,已知销售![]() 只
只![]() 型口罩和
型口罩和![]() 只
只![]() 型口罩的润为
型口罩的润为![]() 元,售
元,售![]() 只
只![]() 型口罩和
型口罩和![]() 只
只![]() 型口罩的利润为
型口罩的利润为![]() 元,
元,
(1)每只![]() 型口罩和
型口罩和![]() 型口罩的利润;
型口罩的利润;
(2)该药店计划一次购进两种型号的口罩![]() 只,其中
只,其中![]() 型口罩的进货量不超过
型口罩的进货量不超过![]() 型口罩的
型口罩的![]() 倍,设购进
倍,设购进![]() 型
型![]() 罩
罩![]() 只,这
只,这![]() 口罩的利润为
口罩的利润为![]() 元;
元;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②药店购进![]() 型口各多少才能使销售总利润最大?
型口各多少才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足( )条件时,四边形EGFH是菱形.
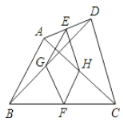
A.AB=CDB.AB//CDC.AB⊥CDD.AB=CD AB//CD
查看答案和解析>>
科目:初中数学 来源: 题型:
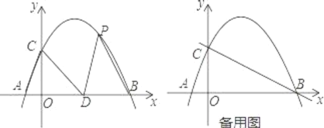
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.
(1)求该抛物线的解析式;
(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;
(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
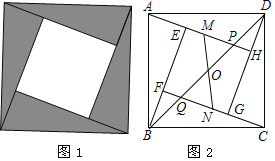
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AE平分∠BAC,交BC于D,交⊙O于E,若AB、AC的长是方程x2-ax+12=0的两实根,AD=2,则AE的长为( )
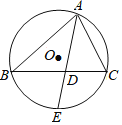
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com