
【题目】如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足( )条件时,四边形EGFH是菱形.
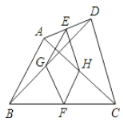
A.AB=CDB.AB//CDC.AB⊥CDD.AB=CD AB//CD
【答案】A
【解析】
E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且等于![]() AB,因此EG∥HF,EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=
AB,因此EG∥HF,EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=![]() CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
需添加条件AB=CD.
证明:∵点E,G分别是AD,BD的中点,
∴EG∥AB,且EG=![]() AB,同理HF∥AB,且HF=
AB,同理HF∥AB,且HF=![]() AB,
AB,
∴EG∥HF,EG=HF,
∴四边形EGFH是平行四边形.
∵EG=![]() AB,同理可得EH=
AB,同理可得EH=![]() CD,
CD,
∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故选:A.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
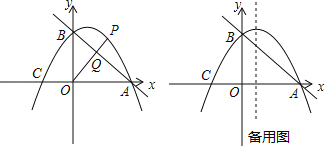
【题目】如图,直线y=﹣![]() x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣
x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为C.
x2+bx+c经过A、B两点,与x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;
(3)点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
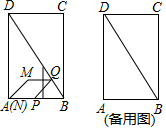
【题目】如图,在矩形ABCD中,AB=2cm,∠ADB=30°.P,Q两点分别从A,B同时出发,点P沿折线AB﹣BC运动,在AB上的速度是2cm/s,在BC上的速度是2![]() cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
(1)当PQ⊥AB时,x等于多少;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)直线AM将矩形ABCD的面积分成1:3两部分时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】便民”水泥代销点销售某种水泥,每吨进价为250元,如果每吨销售价定为290元时,平均每天可售出16吨.
(1)若代销点采取降低促销的方式,试建立每吨的销售利润y(元)与每吨降低x(元)之间的函数关系式;
(2)若每吨售价每降低5元,则平均每天能多售出4吨,问:每吨水泥的实际售价定为多少元时,每天的销售利润平均可达720元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的一点,且
的一点,且![]() ,
,![]() 是
是![]() 上一点,射线
上一点,射线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)当点![]() 为
为![]() 中点时,则
中点时,则![]() ,
,![]() ;(直接写出答案)
;(直接写出答案)
(2)在整个运动过程中,![]() 的值是否会变化,若不变,求出它的值;若变化,请说明理由;
的值是否会变化,若不变,求出它的值;若变化,请说明理由;
(3)若![]() 为等腰三角形时,请求出所有满足条件的
为等腰三角形时,请求出所有满足条件的![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
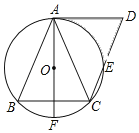
【题目】如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com