
【题目】已知点![]() 与点
与点![]() ,
,![]() ,
,![]() 是一平行四边形的四个顶点,则
是一平行四边形的四个顶点,则![]() 长的最小值是( )
长的最小值是( )
A.10B.![]() C.
C.![]() D.9
D.9
【答案】C
【解析】
①CD是平行四边形的一条边,那么有AB=CD;②CD是平行四边形的一条对角线,过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,证△DBN≌△CAM,推出DN=CM=a-2,BN=AM=8a,得出D(10a,6+a),由勾股定理得:CD2=(10aa)2+(6+a+a-2)2=8a224a+116=8(a![]() )2+98,求出即可.
)2+98,求出即可.
有两种情况:
①CD是平行四边形的一条边,那么有AB=CD=![]() =10
=10
②CD是平行四边形的一条对角线,
过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,

则∠BND=∠DFA=∠CMA=∠QFA=90![]() ,
,
∠CAM+∠FQA=90![]() ,∠BDN+∠DBN=90
,∠BDN+∠DBN=90![]() ,
,
∵四边形ACBD是平行四边形,
∴BD=AC,∠C=∠D,BD∥AC,
∴∠BDF=∠FQA,
∴∠DBN=∠CAM,
∵在△DBN和△CAM中
 ,
,
∴△DBN≌△CAM(AAS),
∴DN=CM=a-2,BN=AM=8a,
D(10a,6+a),
由勾股定理得:CD2=(10aa)2+(6+a+a-2)2=8a224a+116=8(a![]() )2+98,
)2+98,
当a=![]() 时,CD有最小值,是
时,CD有最小值,是![]() =
=![]() ,
,
∵![]() <10,
<10,
∴CD的最小值是![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(-2,m)绕坐标原点O顺时针旋转90°后,恰好落在图中⊙P中的阴影区域(包括边界)内,⊙P的半径为1,点P的坐标为(3,2),则m的取值范围是______.
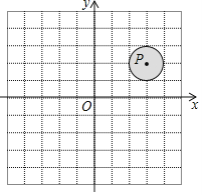
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
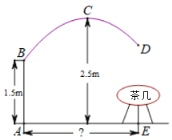
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗疫期间,药店销售![]() 两种类型的口罩,已知销售
两种类型的口罩,已知销售![]() 只
只![]() 型口罩和
型口罩和![]() 只
只![]() 型口罩的润为
型口罩的润为![]() 元,售
元,售![]() 只
只![]() 型口罩和
型口罩和![]() 只
只![]() 型口罩的利润为
型口罩的利润为![]() 元,
元,
(1)每只![]() 型口罩和
型口罩和![]() 型口罩的利润;
型口罩的利润;
(2)该药店计划一次购进两种型号的口罩![]() 只,其中
只,其中![]() 型口罩的进货量不超过
型口罩的进货量不超过![]() 型口罩的
型口罩的![]() 倍,设购进
倍,设购进![]() 型
型![]() 罩
罩![]() 只,这
只,这![]() 口罩的利润为
口罩的利润为![]() 元;
元;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②药店购进![]() 型口各多少才能使销售总利润最大?
型口各多少才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,
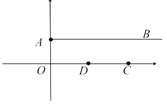
(1)若![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,当
上,当![]() 是边长为5的等腰三角形,共有几个这样的点
是边长为5的等腰三角形,共有几个这样的点![]() ,并尝试求出点
,并尝试求出点![]() 的坐标;
的坐标;
(2)若直线![]() 与
与![]() 不平行,
不平行,![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得
,使得![]() 是直角三角形,且
是直角三角形,且![]() ,若存在,求出这样的点
,若存在,求出这样的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足( )条件时,四边形EGFH是菱形.
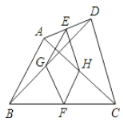
A.AB=CDB.AB//CDC.AB⊥CDD.AB=CD AB//CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AE平分∠BAC,交BC于D,交⊙O于E,若AB、AC的长是方程x2-ax+12=0的两实根,AD=2,则AE的长为( )
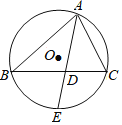
A.5B.6C.7D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com