
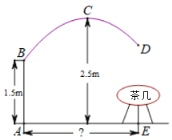
【题目】如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据题意可以把AB所在的直线当作y轴,AE所在的直线当作x轴建立直角坐标系,由防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,点最高点C距灯柱的水平距离为1.6米,可以知道抛物线的顶点坐标C(1.6,2.5),直接设出顶点式y=a(x1.6)2+2.5,然后用待定系数法将(0,1.5)代入解析式解得a值,再次将D点到地面的高当作纵坐标代入解析式即可求出AE的长,将不符合实际的取值舍去即可.
如图,把AB所在的直线当作y轴,AE所在的直线当作x轴建立直角坐标系,由防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,点最高点C距灯柱的水平距离为1.6米,∴抛物线的顶点坐标C(1.6,2.5),
设y=a(x1.6)2+2.5.
由AB得高为1.5米
∴把x=0,y=1.5代入上式得,1.5=a(01.6)2+2.5.
解得,a=![]() .
.
∴y=![]() (x1.6)2+2.5.
(x1.6)2+2.5.
又∵DE的高为1.5米
∴当y=1.5时,则![]() (x1.6)2+2.5=1.5
(x1.6)2+2.5=1.5
解得,x=3.2或x=0(舍去)
∴AE的长为:3.2m,
故选:A.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
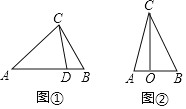
【题目】如图①在![]() 中,若点
中,若点![]() 在边
在边![]() 上,且
上,且![]() 则点
则点![]() 定义为
定义为![]() 的边
的边![]() 上的“金点”.
上的“金点”.
![]() 已知点
已知点![]() 是
是![]() 的边
的边![]() 上的“金点”:
上的“金点”:
①若![]() 则
则![]() 的长为 _;
的长为 _;
②若![]() 则
则![]() 的长为 _;
的长为 _;
![]() 在图①中,若点
在图①中,若点![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]() 试判断点
试判断点![]() 是不是
是不是![]() 的“金
的“金
点”,并说明理由;
![]() 如图②,已知点
如图②,已知点![]() 为同一直线上三点,且
为同一直线上三点,且![]() 在
在![]() 所在直线上是否存在一点
所在直线上是否存在一点![]() 使点
使点![]() 中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段
中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
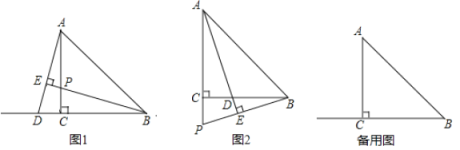
(问题发现)(1)如图1,若点![]() 在
在![]() 的延长线上,试猜想
的延长线上,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系为_______;
之间的数量关系为_______;
(类比探究)(2)如图2,若点![]() 在线段
在线段![]() 上,试猜想
上,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(拓展应用)(3)当点![]() 为
为![]() 的中点时,直接写出线段
的中点时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
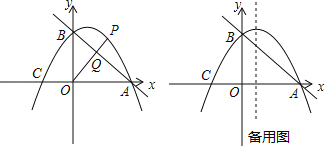
【题目】如图,直线y=﹣![]() x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣
x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为C.
x2+bx+c经过A、B两点,与x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;
(3)点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
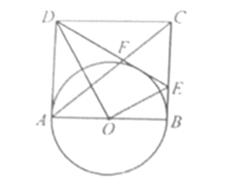
【题目】如图,在矩形![]() 的
的![]() 边上取一点
边上取一点![]() 将
将![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 正好落在
正好落在![]() 边的中点
边的中点![]() 上,
上,![]() 设
设![]() .
.
(1)直接写出![]() 的值和
的值和![]() 的度数;
的度数;
(2)求证:直线![]() 是以
是以![]() 为直径的
为直径的![]() 的切线;
的切线;
(3)连接![]() 交
交![]() 于点
于点![]() 求
求![]() 的边
的边![]() 上的高.
上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
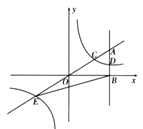
【题目】如图,在平面直角坐标系中,点A的坐标为![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图像的一支分别交
的图像的一支分别交![]() 于点
于点![]() ,延长
,延长![]() 交反比例函数的图像的另一支于点E,已知D的纵坐标为
交反比例函数的图像的另一支于点E,已知D的纵坐标为![]() .
.
(1)求反比例函数的解析式及直线OA的解析式;
(2)连接BC,已知![]() ,求
,求![]()
(3)若在![]() 轴上有两点
轴上有两点![]() ,将直线
,将直线![]() 绕点
绕点![]() 旋转,仍与
旋转,仍与![]() 交于
交于![]() ,能否构成以
,能否构成以![]() 为顶点的四边形为菱形,如果能请求出
为顶点的四边形为菱形,如果能请求出![]() 的值,如果不能说明理由.
的值,如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
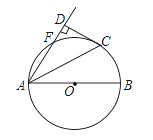
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com