
【题目】如图,在矩形![]() 的
的![]() 边上取一点
边上取一点![]() 将
将![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 正好落在
正好落在![]() 边的中点
边的中点![]() 上,
上,![]() 设
设![]() .
.
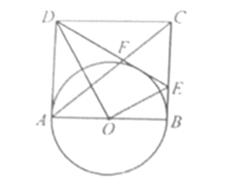
(1)直接写出![]() 的值和
的值和![]() 的度数;
的度数;
(2)求证:直线![]() 是以
是以![]() 为直径的
为直径的![]() 的切线;
的切线;
(3)连接![]() 交
交![]() 于点
于点![]() 求
求![]() 的边
的边![]() 上的高.
上的高.
【答案】(1)![]() ;(2)见详解;(3)
;(2)见详解;(3)![]()
【解析】
(1)由折叠和圆的性质直接可求;
(2)作OG⊥DE于点G,证明△ADO≌△GDO(AAS)即可;
(3)作FH⊥CD于点H,证明△CEF∽△ADF,则有![]() ,再证明△CFH∽△CAD,即可求FH=
,再证明△CFH∽△CAD,即可求FH=![]() .
.
![]() 解:∵O是AB的中点,
解:∵O是AB的中点,
∴OA=OB= ![]() AB=
AB= ![]() ×6=3,
×6=3,
由折叠可得:CD=OD,∠CDE=∠ODE,CE=OE,
∵矩形ABCD,
∴CD=AB=6,BC=AD,∠DAB=∠ABC=90°,
∴OD=6,
∴∠ADO=30°,y=AD=3![]() ,
,
∴BC=3![]() ,
,
在Rt△OBE中,由勾股定理,得
(3![]() x)2=32+x2,
x)2=32+x2,
解得:x=![]() .
.
故答案为x=![]() ,y=3
,y=3![]() ,∠ADO=30°;
,∠ADO=30°;
![]() 证明:作
证明:作![]() 于点
于点![]()
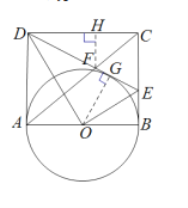
由折叠得![]()
![]()
又![]()
![]()
![]() .
.
![]()
![]() 直线
直线![]() 是
是![]() 的切线.
的切线.
![]() 解:作
解:作![]() 于点
于点![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]() 即
即![]() 的边
的边![]() 上的高为
上的高为![]()


科目:初中数学 来源: 题型:
【题目】为加强公民节电意识,某县将居民用电量分为两个阶梯,月用电量不超过![]() 度时按第一个阶梯费用收费,超过
度时按第一个阶梯费用收费,超过![]() 度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 3月 |
用电量 |
|
金额 |
|
2019年3月收费员林云
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 4月 |
用电量 |
|
金额 |
|
2019年4月收费员林云
查看答案和解析>>
科目:初中数学 来源: 题型:
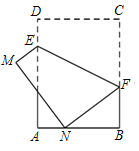
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E,F分别为边AD,BC上的一个动点,连接EF,以EF为对称轴折叠四边形CDEF,得到四边形MNFE,点D,C的对应点分别为M,N,当点N恰好落在AB的三等分点时,CF的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c与x轴交于A,B两点(点A在B左边),与y轴交于点C.
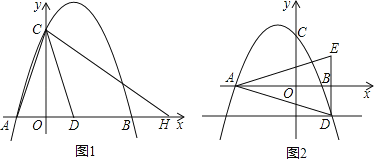
(1)如图1,已知A(﹣1,0),B(3,0).
①直接写出抛物线的解析式;
②点H在x轴上,D(1,0),连接AC,DC,HC,若CD平分∠ACH,求点H的坐标;
(2)如图2,直线y=﹣1与抛物线y=﹣x2+bx+c交于点D,点E,D关于x轴对称.
①若点D在抛物线对称轴的右侧,求证:DB⊥AE;
②若点D在抛物线对称轴的左侧,请直接判断,BD是否垂直AE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
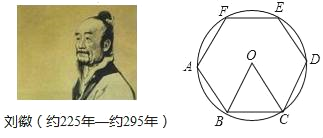
查看答案和解析>>
科目:初中数学 来源: 题型:
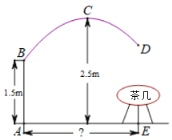
【题目】如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为多少米( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月26日11:30,全球新冠肺炎确诊病例突破47万例,已有60个国家宣布进入紧急状态,国外较多医护人员不得不重复使用一次性口罩和防护装备.深圳海王星辰福田某药店购进A、B两种一次性口罩共1500个,已知购进A种一次性口罩和B种一次性口罩的费用分别为3000元和2000元,且A种一次性口罩的单价比B种一次性口罩单价多1元,求A、B两种一次性口罩的单价各是多少?设A种一次性口罩单价为x元,根据题意,列方程正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
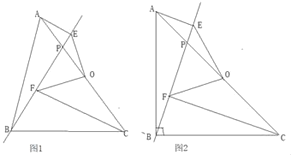
【题目】在△ABC中, AB=BC,O是AC的中点,P是AC上的一个动点(P点不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,判断线段OE与OF的数量关系是什么,请说明理由;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com