
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
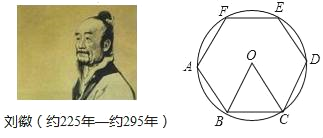
【答案】3.12
【解析】
连接OA1、OA2,根据正十二边形的性质得到∠A1OA2=30°,△A1OA2是等腰三角形,作OM⊥A1A2于M,根据等腰三角形三线合一的性质得出∠A1OM=15°,A1A2=2A1M.设圆的半径R,解直角△A1OM,求出A1M,进而得到正十二边形的周长L,那么圆周率π≈![]() .
.
如图,设半径为R的圆内接正十二边形的周长为L.
连接OA1、OA2,
∵十二边形A1A2…A12是正十二边形,
∴∠A1OA2=30°.
作OM⊥A1A2于M,又OA1=OA2,
∴∠A1OM=15°,A1A2=2A1M.
在直角△A1OM中,A1M=OA1sin∠A1OM=0.26R,
∴A1A2=2A1M=0.52R,
∴L=12A1A2=6.24R,
∴圆周率π≈![]() =
=![]() =3.12.
=3.12.
故答案为3.12.


科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系中,任意两点![]() ,
,![]() 之间的位置关系有以下三种情形;
之间的位置关系有以下三种情形;
①如果![]() 轴,则
轴,则![]() ,
,![]()
②如果![]() 轴,则
轴,则![]() ,
,![]()
③如果![]() 与
与![]() 轴、
轴、![]() 轴均不平行,如图,过点
轴均不平行,如图,过点![]() 作与
作与![]() 轴的平行线与过点
轴的平行线与过点![]() 作与
作与![]() 轴的平行线相交于点
轴的平行线相交于点![]() ,则点
,则点![]() 坐标为
坐标为![]() ,由①得
,由①得![]() ;由②得
;由②得![]() ;根据勾股定理可得平面直角坐标系中任意两点的距离公式
;根据勾股定理可得平面直角坐标系中任意两点的距离公式![]() .
.
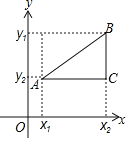
(1)若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() 则
则![]() ________;
________;
(2)若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的动点,直接写出
轴上的动点,直接写出![]() 最小值=_______;
最小值=_______;
(3)已知![]() ,
,![]() 根据数形结合,求出
根据数形结合,求出![]() 的最小值?
的最小值?![]() 的最大值?
的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级10个班的300名学生即将参加学校举行的研究旅行活动,学校提出以下4个活动主题:A.赤水丹霞地貌考察;B.平塘天文知识考察;C.山关红色文化考察;D.海龙电土司文化考察,为了解学生喜欢的活动主题,学生会开展了一次调查研究,请将下面的过程补全
(1)收集数据:学生会计划调查学生喜欢的活动主题情况,下面抽样调查的对象选择合理的是______.(填序号)
①选择七年级3班、4班、5班学生作为调查对象
②选择学校旅游摄影社团的学生作为调查对象
③选择各班学号为6的倍数的学生作为调查对象
(2)整理、描述数据:通过调査后,学生会同学绘制了如下两幅不完整的统计图,请把统计图补充完整
某校七年级学生喜欢的活动主题条形统计图某校七年级学生喜欢的活动主题扇形统计图
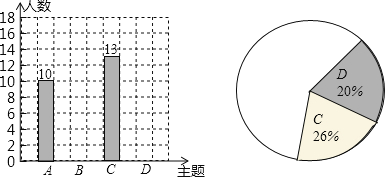
(3)分析数据、推断结论:请你根据上述调查结果向学校推荐本次活动的主题,你的推荐是______(填A-D的字母代号),估算全年级大约有多少名学生喜欢这个主题活动
(4)若在5名学生会干部(3男2女)中,随机选取2名同学担任活动的组长和副组长,求抽出的两名同学恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学进行社会调查,随机抽查了某个小区的200户家庭的年收入,并绘制成统计图(如图).请你根据统计图给出的信息回答:
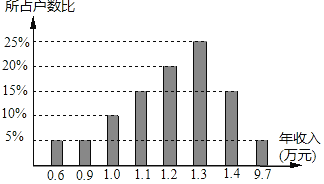
(1)样本数据的中位数是_____,众数是_____;
(2)这200户家庭的平均年收入为_____万元;
(3)在平均数、中位数两数中,_____更能反映这个小区家庭的年收入水平.
(4)如果该小区有1200户住户,请你根据抽样调查的结果估计该小区有_____户家庭的年收入低于1.3万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;
⑤5a﹣2b+c<0.
其中正确的个数有( )
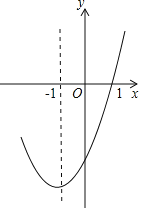
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 的
的![]() 边上取一点
边上取一点![]() 将
将![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 正好落在
正好落在![]() 边的中点
边的中点![]() 上,
上,![]() 设
设![]() .
.
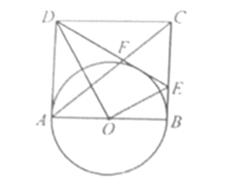
(1)直接写出![]() 的值和
的值和![]() 的度数;
的度数;
(2)求证:直线![]() 是以
是以![]() 为直径的
为直径的![]() 的切线;
的切线;
(3)连接![]() 交
交![]() 于点
于点![]() 求
求![]() 的边
的边![]() 上的高.
上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有两点![]() ,它们的对应数分别是
,它们的对应数分别是![]() ,其中
,其中![]()
![]()
(1)在![]() 左侧作线段
左侧作线段![]() ,在
,在![]() 的右侧作线段
的右侧作线段![]() (要求尺规作图,不写作法,保留作图痕迹)
(要求尺规作图,不写作法,保留作图痕迹)
(2)若点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() ,且
,且![]() ,求
,求![]() 的值
的值
(3)在(2)的条件下,设点![]() 是
是![]() 的中点,
的中点,![]() 是数轴上一点,且
是数轴上一点,且![]() ,请直接写出
,请直接写出![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为且在
为且在![]() 的右侧作正方形
的右侧作正方形![]() .
.

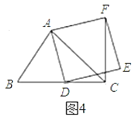
(1)如果![]() ,当点
,当点![]() 在线段BC上时(与点
在线段BC上时(与点![]() 不重合),①如图2,线段
不重合),①如图2,线段![]() 的数量关系为 ,线段
的数量关系为 ,线段![]() 所在直线的位置关系为 ;
所在直线的位置关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如,3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如,3,①中的结论是否仍然成立,并说明理由;
(2)如图4,如果![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),请直接写出答案.
不重合),请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com