
【题目】阅读理解:在平面直角坐标系中,任意两点![]() ,
,![]() 之间的位置关系有以下三种情形;
之间的位置关系有以下三种情形;
①如果![]() 轴,则
轴,则![]() ,
,![]()
②如果![]() 轴,则
轴,则![]() ,
,![]()
③如果![]() 与
与![]() 轴、
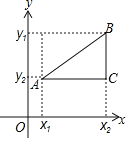
轴、![]() 轴均不平行,如图,过点
轴均不平行,如图,过点![]() 作与
作与![]() 轴的平行线与过点
轴的平行线与过点![]() 作与
作与![]() 轴的平行线相交于点
轴的平行线相交于点![]() ,则点
,则点![]() 坐标为
坐标为![]() ,由①得
,由①得![]() ;由②得
;由②得![]() ;根据勾股定理可得平面直角坐标系中任意两点的距离公式
;根据勾股定理可得平面直角坐标系中任意两点的距离公式![]() .
.
(1)若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() 则
则![]() ________;
________;
(2)若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的动点,直接写出
轴上的动点,直接写出![]() 最小值=_______;
最小值=_______;
(3)已知![]() ,
,![]() 根据数形结合,求出
根据数形结合,求出![]() 的最小值?
的最小值?![]() 的最大值?
的最大值?
【答案】(1)5;(2)3![]() ;(3)M最小值=
;(3)M最小值=![]() ,N最大值=
,N最大值=![]() .
.
【解析】
(1)利用两点间的距离公式AB=![]() 计算;
计算;
(2)利用轴对称的性质求得点P的坐标以及AP+PB的最小值;
(3)利用M、N所表示的几何意义解答.
解:(1)AB=![]() =5;
=5;
故答案是:5;
(2)如图,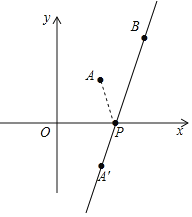
∵点A坐标为(3,3),
∴点A关于x轴对称的点A′的坐标是(3,-3),
此时AP+PB=A′B=![]() ,
,
故答案是:3![]() ;
;
(3)M=![]() ,
,
当M取最小值时,M表示点(x,0)与点(6,4)的距离与点(x,0)与点 (3,2)的距离之和(或M表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,-2)的距离之和),
此时M最小值=![]() ,
,
N=![]() ,当N取最大值时,N表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差(或M表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差),
,当N取最大值时,N表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差(或M表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差),
此时N最大值=![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,若二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() (-1,0)、
(-1,0)、![]() ,与
,与![]() 轴交于点
轴交于点![]() (0,4),连接
(0,4),连接![]() 、
、![]() ,且抛物线的对称轴为直线
,且抛物线的对称轴为直线![]() .
.
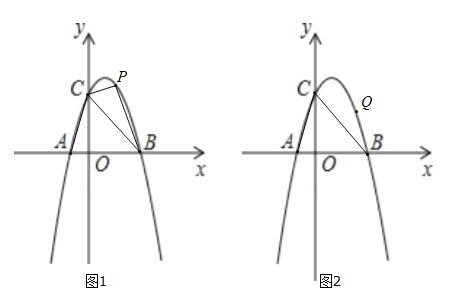
(1)求二次函数的解析式;
(2)若点![]() 是抛物线在一象限内
是抛物线在一象限内![]() 上方一动点,且点
上方一动点,且点![]() 在对称轴的右侧,连接
在对称轴的右侧,连接![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)如图2,若点![]() 是抛物线上一动点,且满足
是抛物线上一动点,且满足![]() ,请直接写出点
,请直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某交为了开展“阳光体育运动”,计划购买篮球和足球,已知足球的单价比篮球的单价多![]() 元.若购买
元.若购买![]() 个篮球和
个篮球和![]() 个足球需花费
个足球需花费![]() 元.
元.
(1)求篮球和足球的单价各是多少元;
(2)若学校购买篮球和足球共![]() 个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
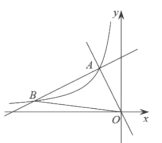
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强公民节电意识,某县将居民用电量分为两个阶梯,月用电量不超过![]() 度时按第一个阶梯费用收费,超过
度时按第一个阶梯费用收费,超过![]() 度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 3月 |
用电量 |
|
金额 |
|
2019年3月收费员林云
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 4月 |
用电量 |
|
金额 |
|
2019年4月收费员林云
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.
(1)如图1,求证:∠CAE=∠CBD;
(2)如图2,F是BD的中点,求证:AE⊥CF;
(3)如图3,F,G分别是BD,AE的中点,若AC=2![]() ,CE=1,求△CGF的面积.
,CE=1,求△CGF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
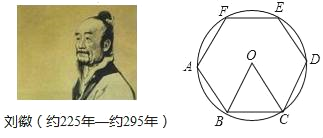
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com