
”¾ĢāÄæ”æĪŖ¼ÓĒ湫Ćń½ŚµēŅāŹ¶£¬Ä³ĻŲ½«¾ÓĆńÓƵēĮæ·ÖĪŖĮ½øö½×ĢŻ£¬ŌĀÓƵēĮæ²»³¬¹ż![]() ¶ČŹ±°“µŚŅ»øö½×ĢŻ·ŃÓĆŹÕ·Ń£¬³¬¹ż
¶ČŹ±°“µŚŅ»øö½×ĢŻ·ŃÓĆŹÕ·Ń£¬³¬¹ż![]() ¶ČŹ±£¬³¬³öµÄ²æ·Ö°“µŚ¶žøö½×ĢŻ·ŃÓĆŹÕ·ŃĻĀ±ķŹĒøĆĻŲ¾ÓĆńŠ¤Ī°¼Ņ2019Äź3ŌĀŗĶ4ŌĀĖł½»µē·ŃµÄŹÕ¾Ż£®ĒóøĆĻŲ¾ÓĆńÓƵēµŚ--½×ĢŻµē·ŃŗĶµŚ¶ž½×ĢŻµē·Ń·Ö±šĪŖĆæ¶Č¶ąÉŁŌŖ£æ
¶ČŹ±£¬³¬³öµÄ²æ·Ö°“µŚ¶žøö½×ĢŻ·ŃÓĆŹÕ·ŃĻĀ±ķŹĒøĆĻŲ¾ÓĆńŠ¤Ī°¼Ņ2019Äź3ŌĀŗĶ4ŌĀĖł½»µē·ŃµÄŹÕ¾Ż£®ĒóøĆĻŲ¾ÓĆńÓƵēµŚ--½×ĢŻµē·ŃŗĶµŚ¶ž½×ĢŻµē·Ń·Ö±šĪŖĆæ¶Č¶ąÉŁŌŖ£æ
µē·ŃŹÕ¾Ż£ØŠŅø£ĄļŠ”Ēųµē·Ń×ØÓĆÕĀ£©
»§Ćū | Š¤Ī° |
µē±ķŗÅ |
|
ŌĀ·Ż | 3ŌĀ |
ÓƵēĮæ |
|
½š¶ī |
|
2019Äź3ŌĀŹÕ·ŃŌ±ĮÖŌĘ
µē·ŃŹÕ¾Ż£ØŠŅø£ĄļŠ”Ēųµē·Ń×ØÓĆÕĀ£©
»§Ćū | Š¤Ī° |
µē±ķŗÅ |
|
ŌĀ·Ż | 4ŌĀ |
ÓƵēĮæ |
|
½š¶ī |
|
2019Äź4ŌĀŹÕ·ŃŌ±ĮÖŌĘ
”¾“š°ø”æøĆĻŲµŚŅ»½×ĢŻµē·ŃĪŖĆæ¶Č![]() ŌŖ£¬µŚ¶ž½×ĢŻµē·ŃĪŖĆæ¶Č
ŌŖ£¬µŚ¶ž½×ĢŻµē·ŃĪŖĆæ¶Č![]() ŌŖ£®
ŌŖ£®
”¾½āĪö”æ
ÉčøĆĻŲ¾ÓĆńÓƵēµŚŅ»½×ĢŻµē·ŃĆæ¶ČxŌŖ£¬µŚ¶ž½×ĢŻµē·ŃĆæ¶ČyŌŖ£¬øł¾ŻŠ¤Ī°¼Ņ2019Äź3ŌĀŗĶ4ŌĀĖł½»µē·ŃµÄŹÕ¾Ż£¬¼“æÉµĆ³ö¹ŲÓŚx£¬yµÄ¶žŌŖŅ»“Ī·½³Ģ×飬½āÖ®¼“æÉµĆ³ö½įĀŪ£®
ÉčøĆĻŲµŚŅ»½×ĢŻµē·ŃĪŖĆæ¶Č![]() ŌŖ£¬µŚ¶ž½×ĢŻµē·ŃĪŖĆæ¶Č
ŌŖ£¬µŚ¶ž½×ĢŻµē·ŃĪŖĆæ¶Č![]() ŌŖ£¬
ŌŖ£¬
ÓÉĢāŅāæÉµĆ£¬
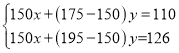
½āµĆ![]()
¹ŹøĆĻŲµŚŅ»½×ĢŻµē·ŃĪŖĆæ¶Č![]() ŌŖ£®µŚ¶ž½×ĢŻµē·ŃĪŖĆæ¶Č
ŌŖ£®µŚ¶ž½×ĢŻµē·ŃĪŖĆæ¶Č![]() ŌŖ
ŌŖ



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖµćA(©3£¬y1)£¬B(2£¬y2)¾łŌŚÅ×ĪļĻßy£½ax2+bx+cÉĻ£¬µćP(m£¬n)ŹĒøĆÅ×ĪļĻߵĶ„µć£¬Čōy1£¾y2”Żn£¬ŌņmµÄȔֵ·¶Ī§ŹĒ(””””)
A.©3£¼m£¼2B.©![]() £¼m£¼-
£¼m£¼-![]() C.m£¾©
C.m£¾©![]() D.m£¾2
D.m£¾2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µć A µÄ×ų±źŹĒ£Ø©2£¬0£©£¬µć B µÄ×ų±źŹĒ£Ø0£¬6£©£¬C ĪŖ OB µÄÖŠµć£¬½«”÷ABC Čʵć B ÄꏱÕėŠż×Ŗ 90”ćŗóµĆµ½”÷A”äB”äC”䣮Čō·“±ČĄżŗÆŹż y ![]() µÄĶ¼ĻóĒ”ŗĆ¾¹ż A”äB µÄÖŠµć D£¬Ōņk _________£®
µÄĶ¼ĻóĒ”ŗĆ¾¹ż A”äB µÄÖŠµć D£¬Ōņk _________£®
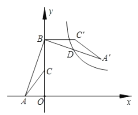
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
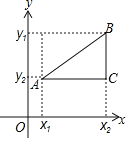
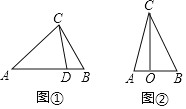
”¾ĢāÄæ”æČēĶ¼1ŗĶĶ¼2£¬ŌŚ”÷ABCÖŠ£¬AB£½13£¬BC£½14£¬![]() .
.
Ģ½¾æ£ŗČēĶ¼1£¬AH”ĶBCÓŚµćH£¬ŌņAH£½___£¬AC£½___£¬”÷ABCµÄĆ껿![]() £½___.
£½___.
ĶŲÕ¹£ŗČēĶ¼2£¬µćDŌŚACÉĻ£ØæÉÓėµćA”¢CÖŲŗĻ£©£¬·Ö±š¹żµćA”¢C×÷Ö±ĻßBDµÄ“¹Ļߣ¬“¹×ćĪŖE”¢F£¬ÉčBD£½x£¬AE£½m£¬CF£½n£¬£Øµ±µćDÓėAÖŲŗĻŹ±£¬ĪŅĆĒČĻĪŖ![]() £½0£©.
£½0£©.
£Ø1£©ÓĆŗ¬x”¢m»ņnµÄ“śŹżŹ½±ķŹ¾![]() ¼°
¼°![]() £»
£»
£Ø2£©Ēó(m+n)ÓėxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó(m+n)µÄ×ī“óÖµŗĶ×īŠ”Öµ£»
£Ø3£©¶Ōøų¶ØµÄŅ»øöxÖµ£¬ÓŠŹ±Ö»ÄÜČ·¶ØĪØŅ»µÄµćD£¬Öø³öÕāŃłµÄxµÄȔֵ·¶Ī§.
·¢ĻÖ£ŗĒėÄćČ·¶ØŅ»ĢõÖ±Ļߣ¬Ź¹µĆA”¢B”¢CČżµćµ½ÕāĢõÖ±ĻߵľąĄėÖ®ŗĶ×īŠ”£Ø²»±ŲŠ“³ö¹ż³Ģ£©£¬²¢Š“³öÕāøö×īŠ”Öµ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĄķ½ā£ŗŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ČĪŅāĮ½µć![]() £¬
£¬![]() Ö®¼äµÄĪ»ÖĆ¹ŲĻµÓŠŅŌĻĀČżÖÖĒéŠĪ£»
Ö®¼äµÄĪ»ÖĆ¹ŲĻµÓŠŅŌĻĀČżÖÖĒéŠĪ£»
¢ŁČē¹ū![]() Öį£¬Ōņ
Öį£¬Ōņ![]() £¬
£¬![]()
¢ŚČē¹ū![]() Öį£¬Ōņ
Öį£¬Ōņ![]() £¬
£¬![]()
¢ŪČē¹ū![]() Óė
Óė![]() Öį”¢
Öį”¢![]() Öį¾ł²»Ę½ŠŠ£¬ČēĶ¼£¬¹żµć
Öį¾ł²»Ę½ŠŠ£¬ČēĶ¼£¬¹żµć![]() ×÷Óė
×÷Óė![]() ÖįµÄĘ½ŠŠĻßÓė¹żµć
ÖįµÄĘ½ŠŠĻßÓė¹żµć![]() ×÷Óė
×÷Óė![]() ÖįµÄĘ½ŠŠĻßĻą½»ÓŚµć
ÖįµÄĘ½ŠŠĻßĻą½»ÓŚµć![]() £¬Ōņµć
£¬Ōņµć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬ÓÉ¢ŁµĆ
£¬ÓÉ¢ŁµĆ![]() £»ÓÉ¢ŚµĆ
£»ÓÉ¢ŚµĆ![]() £»øł¾Ż¹“¹É¶ØĄķæɵĆĘ½ĆęÖ±½Ē×ų±źĻµÖŠČĪŅāĮ½µćµÄ¾ąĄė¹«Ź½
£»øł¾Ż¹“¹É¶ØĄķæɵĆĘ½ĆęÖ±½Ē×ų±źĻµÖŠČĪŅāĮ½µćµÄ¾ąĄė¹«Ź½![]() £®
£®
£Ø1£©Čōµć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬µć
£¬µć![]() ×ų±źĪŖ
×ų±źĪŖ![]() Ōņ
Ōņ![]() ________£»
________£»
£Ø2£©Čōµć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬µć
£¬µć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬µć
£¬µć![]() ŹĒ
ŹĒ![]() ÖįÉĻµÄ¶Æµć£¬Ö±½ÓŠ“³ö
ÖįÉĻµÄ¶Æµć£¬Ö±½ÓŠ“³ö![]() ×īŠ”Öµ=_______£»
×īŠ”Öµ=_______£»
£Ø3£©ŅŃÖŖ![]() £¬
£¬![]() øł¾ŻŹżŠĪ½įŗĻ£¬Ēó³ö
øł¾ŻŹżŠĪ½įŗĻ£¬Ēó³ö![]() µÄ×īŠ”Öµ£æ
µÄ×īŠ”Öµ£æ![]() µÄ×ī“óÖµ£æ
µÄ×ī“óÖµ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢ŁŌŚ![]() ÖŠ£¬Čōµć
ÖŠ£¬Čōµć![]() ŌŚ±ß
ŌŚ±ß![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() Ōņµć
Ōņµć![]() ¶ØŅåĪŖ
¶ØŅåĪŖ![]() µÄ±ß
µÄ±ß![]() ÉĻµÄ”°½šµć”±£®
ÉĻµÄ”°½šµć”±£®
![]() ŅŃÖŖµć
ŅŃÖŖµć![]() ŹĒ
ŹĒ![]() µÄ±ß
µÄ±ß![]() ÉĻµÄ”°½šµć”±:
ÉĻµÄ”°½šµć”±:
¢ŁČō![]() Ōņ
Ōņ![]() µÄ³¤ĪŖ _£»
µÄ³¤ĪŖ _£»
¢ŚČō![]() Ōņ
Ōņ![]() µÄ³¤ĪŖ _£»
µÄ³¤ĪŖ _£»
![]() ŌŚĶ¼¢ŁÖŠ£¬Čōµć
ŌŚĶ¼¢ŁÖŠ£¬Čōµć![]() ŹĒ
ŹĒ![]() µÄ±ß
µÄ±ß![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() ŹŌÅŠ¶Ļµć
ŹŌÅŠ¶Ļµć![]() ŹĒ²»ŹĒ
ŹĒ²»ŹĒ![]() µÄ”°½š
µÄ”°½š
µć”±£¬²¢ĖµĆ÷ĄķÓÉ£»
![]() ČēĶ¼¢Ś£¬ŅŃÖŖµć
ČēĶ¼¢Ś£¬ŅŃÖŖµć![]() ĪŖĶ¬Ņ»Ö±ĻßÉĻČżµć£¬ĒŅ
ĪŖĶ¬Ņ»Ö±ĻßÉĻČżµć£¬ĒŅ![]() ŌŚ
ŌŚ![]() ĖłŌŚÖ±ĻßÉĻŹĒ·ń“ęŌŚŅ»µć
ĖłŌŚÖ±ĻßÉĻŹĒ·ń“ęŌŚŅ»µć![]() Ź¹µć
Ź¹µć![]() ÖŠµÄijŅ»µćŹĒĘäӹȿµćĪ§³ÉµÄČż½ĒŠĪµÄ”°½šµć”±£®Čō“ęŌŚ£¬Ēó³öĻ߶Ī
ÖŠµÄijŅ»µćŹĒĘäӹȿµćĪ§³ÉµÄČż½ĒŠĪµÄ”°½šµć”±£®Čō“ęŌŚ£¬Ēó³öĻ߶Ī![]() µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóµÄŅ»Ö§Ī»ÓŚµŚŅ»ĻóĻŽ£®
µÄĶ¼ĻóµÄŅ»Ö§Ī»ÓŚµŚŅ»ĻóĻŽ£®
£Ø1£©ÅŠ¶ĻøĆŗÆŹżĶ¼ĻóµÄĮķŅ»Ö§ĖłŌŚµÄĻóĻŽ£¬²¢ĒómµÄȔֵ·¶Ī§£»
£Ø2£©ČēĶ¼£¬OĪŖ×ų±źŌµć£¬µćAŌŚøĆ·“±ČĄżŗÆŹżĪ»ÓŚµŚŅ»ĻóĻŽµÄĶ¼ĻóÉĻ£¬µćBÓėµćA¹ŲÓŚ![]() Öį¶Ō³Ę£¬Čō”÷OABµÄĆ껿ĪŖ6£¬ĒómµÄÖµ£®
Öį¶Ō³Ę£¬Čō”÷OABµÄĆ껿ĪŖ6£¬ĒómµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬Å×ĪļĻßy£½-![]() x2+
x2+![]() x+
x+![]() ÓėxÖį½»ÓŚA”¢BĮ½µć(µćAŌŚµćBµÄ×ó²ą)£¬½»yÖįÓŚµćC£®½«Ö±ĻßACŅŌµćAĪŖŠż×ŖÖŠŠÄ£¬Ė³Ź±ÕėŠż×Ŗ90”ć£¬½»yÖįÓŚµćD£¬½»ĪļĻßÓŚĮķŅ»µćE£®
ÓėxÖį½»ÓŚA”¢BĮ½µć(µćAŌŚµćBµÄ×ó²ą)£¬½»yÖįÓŚµćC£®½«Ö±ĻßACŅŌµćAĪŖŠż×ŖÖŠŠÄ£¬Ė³Ź±ÕėŠż×Ŗ90”ć£¬½»yÖįÓŚµćD£¬½»ĪļĻßÓŚĮķŅ»µćE£®
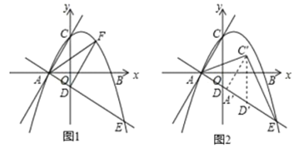
(1)ĒóÖ±ĻßAEµÄ½āĪöŹ½£»
(2)µćFŹĒµŚŅ»ĻóĻŽÄŚÅ×ĪļĻßÉĻŅ»µć£¬µ±”÷FADµÄĆ껿×ī“óŹ±£¬Ēó³ö“ĖŹ±µćFµÄ×ų±ź£»
(3)ČēĶ¼2£¬½«”÷ACDŃŲÉäĻßAE·½ĻņŅŌĆæĆė![]() øöµ„Ī»µÄĖŁ¶ČĘ½ŅĘ£¬¼ĒĘ½ŅĘŗóµÄ”÷ACDĪŖ”÷A”äC”äD”ä£¬Ę½ŅĘŹ±¼äĪŖtĆė£¬µ±”÷AC”äEĪŖµČŃüČż½ĒŠĪŹ±£¬ĒótµÄÖµ£®
øöµ„Ī»µÄĖŁ¶ČĘ½ŅĘ£¬¼ĒĘ½ŅĘŗóµÄ”÷ACDĪŖ”÷A”äC”äD”ä£¬Ę½ŅĘŹ±¼äĪŖtĆė£¬µ±”÷AC”äEĪŖµČŃüČż½ĒŠĪŹ±£¬ĒótµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪ![]() µÄ
µÄ![]() ±ßÉĻČ”Ņ»µć
±ßÉĻČ”Ņ»µć![]() ½«
½«![]() ŃŲ
ŃŲ![]() ÕŪµž£¬¶„µć
ÕŪµž£¬¶„µć![]() ÕżŗĆĀäŌŚ
ÕżŗĆĀäŌŚ![]() ±ßµÄÖŠµć
±ßµÄÖŠµć![]() ÉĻ£¬
ÉĻ£¬![]() Éč
Éč![]() £®
£®
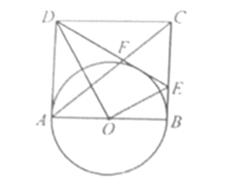
£Ø1£©Ö±½ÓŠ“³ö![]() µÄÖµŗĶ
µÄÖµŗĶ![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
£Ø2£©ĒóÖ¤£ŗÖ±Ļß![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖÖ±¾¶µÄ
ĪŖÖ±¾¶µÄ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
£Ø3£©Į¬½Ó![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() Ēó
Ēó![]() µÄ±ß
µÄ±ß![]() ÉĻµÄøߣ®
ÉĻµÄøߣ®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com