
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;
⑤5a﹣2b+c<0.
其中正确的个数有( )
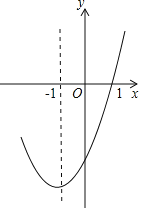
A. 2 B. 3 C. 4 D. 5
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图有一长条型链子,其外形由边长为![]() 的正六边形排列而成.其中每个黑色六边形与6个白色六边形相邻,若链子上有35个黑色六边形,则此链子有( )个白色六边形.
的正六边形排列而成.其中每个黑色六边形与6个白色六边形相邻,若链子上有35个黑色六边形,则此链子有( )个白色六边形.

A.140B.142C.208D.210
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
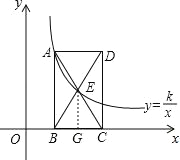
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个生产生活现象,可以用“两点之间,线段最短”来解释的是( )
A.用两颗钉子就可以把木条固定在墙上
B.从![]() 地到
地到![]() 地架设电线沿线段
地架设电线沿线段![]() 来架设
来架设
C.植树时定出两棵树的位置后确定同一行树所在的直线
D.打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
查看答案和解析>>
科目:初中数学 来源: 题型:
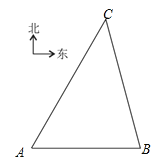
【题目】如图所示,为测量旗台A与图书馆C之间的直线距离,小明在A处测得C在北偏东30°方向上,然后向正东方向前进100米至B处,测得此时C在北偏西15°方向上,求旗台与图书馆之间的距离.(结果精确到1米,参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .
.
(1)![]() 满足何条件时,y随x的增大而减小;
满足何条件时,y随x的增大而减小;
(2)![]() 满足何条件时,图像经过第一、二、四象限;
满足何条件时,图像经过第一、二、四象限;
(3)![]() 满足何条件时,它的图像与y轴的交点在x轴的上方.
满足何条件时,它的图像与y轴的交点在x轴的上方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:第20个“上”字需用多少枚棋子( )

A. 78 B. 82 C. 86 D. 90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
小明和小丽共同探究一道数学题:
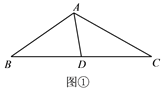
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,
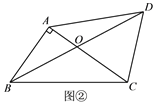
AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com