【题目】如图，是用棋子摆成的“上”字：如果按照以上规律继续摆下去，那么通过观察，可以发现：第20个“上”字需用多少枚棋子（ ）
A. 78 B. 82 C. 86 D. 90
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：
①abc＞0；
②b2﹣4ac＞0；
③9a﹣3b+c=0；
④若点（﹣0.5，y1），（﹣2，y2）均在抛物线上，则y1＞y2；
⑤5a﹣2b+c＜0．
其中正确的个数有（ ）
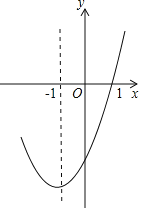
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1：y=2x+1与直线l2：y=mx+4相交于点P（1，b）
(1)求b，m的值
(2)垂直于x轴的直线x=a与直线l1，l2分别相交于C，D，若线段CD长为2，求a的值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O直径，P点为半径OA上异于O点和A点的一个点，过P点作与直径AB垂直的弦CD，连接AD，作BE⊥AB，OE∥AD交BE于E点，连接AE、DE、AE交CD于F点．
（1）求证：DE为⊙O切线；
（2）若⊙O的半径为3，sin∠ADP=
，求AD；
（3）请猜想PF与FD的数量关系，并加以证明．
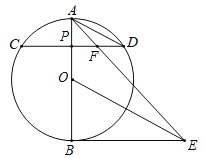
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设直线y＝kx+6和直线y＝（k+1）x+6（k是正整数）及x轴围成的三角形面积为Sk（k＝1，2，3，…，8），则S1+S2+S3+…+S8的值是（ ）
A. 
B. 
C. 16D. 14
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知n边形的内角和θ=（n-2）×180°.
（1）甲同学说，θ能取360°；而乙同学说，θ也能取630°.甲、乙的说法对吗？若对，求出边数n.若不对，说明理由；
（2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在长方形
中，
10厘米，
6厘米，点
沿
边从点
开始向点
以2厘米/秒的速度移动;点
沿
边从点
开始向点以1厘米/秒的速度移动．如果
同时出发，用
(秒)表示移动的时间．那么：
(1)如图1，用含的代数式表示
和
，若线段
，求的值．
(2)如图2，在不考虑点的情况下，连接
，用含t的代数式表示△QAB的面积．
(3)图2中，若△QAB的面积等于长方形的面积的
，求的值．
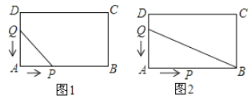
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面文字，然后回答问题．
大家知道
是无理数，而无理数是无限不循环小数，所以的小数部分我们不可能全部写出来，由于的整数部分是1，将 减去它的整数部分，差就是它的小数部分，因此的小数部分可用﹣1表示．
由此我们得到一个真命题：如果＝x+y，其中x是整数，且0＜y＜1，那么x＝1，y＝﹣1．
请解答下列问题：
（1）如果
＝a+b，其中a是整数，且0＜b＜1，那么a＝ ，b＝ ；
（2）如果﹣＝c+d，其中c是整数，且0＜d＜1，那么c＝ ，d＝ ；
（3）已知2+＝m+n，其中m是整數，且0＜n＜1，求|m﹣n|的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
