
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
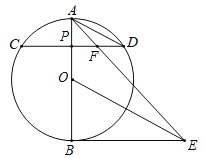
【答案】(1)证明见解析;(2)2;(3)PF=FD,证明见解析.
【解析】(1)如图1,连接OD、BD,根据圆周角定理得:∠ADB=90°,则AD⊥BD,OE⊥BD,由垂径定理得:BM=DM,证明△BOE≌△DOE,则∠ODE=∠OBE=90°,可得结论;
(2)设AP=a,根据三角函数得:AD=3a,由勾股定理得:PD=2![]() a,在直角△OPD中,根据勾股定理列方程可得:32=(3-a)2+(2
a,在直角△OPD中,根据勾股定理列方程可得:32=(3-a)2+(2![]() a)2,解出a的值可得AD的值;
a)2,解出a的值可得AD的值;
(3)先证明△APF∽△ABE,得![]() ,由△ADP∽△OEB,得
,由△ADP∽△OEB,得![]() ,可得PD=2PF,可得结论.
,可得PD=2PF,可得结论.
详证明:(1)如图1,连接OD、BD,BD交OE于M,
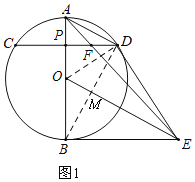
∵AB是⊙O的直径,
∴∠ADB=90°,AD⊥BD,
∵OE∥AD,
∴OE⊥BD,
∴BM=DM,
∵OB=OD,
∴∠BOM=∠DOM,
∵OE=OE,
∴△BOE≌△DOE(SAS),
∴∠ODE=∠OBE=90°,
∴DE为⊙O切线;
(2)设AP=a,
∵sin∠ADP=![]() ,
,
∴AD=3a,
∴PD=![]() ,
,
∵OP=3-a,
∴OD2=OP2+PD2,
∴32=(3-a)2+(2![]() a)2,
a)2,
9=9-6a+a2+8a2,
a1=![]() ,a2=0(舍),
,a2=0(舍),
当a=![]() 时,AD=3a=2,
时,AD=3a=2,
∴AD=2;
(3)PF=FD,
理由是:∵∠APD=∠ABE=90°,∠PAD=∠BAE,
∴△APF∽△ABE,
∴![]() ,
,
∴PF=![]() ,
,
∵OE∥AD,
∴∠BOE=∠PAD,
∵∠OBE=∠APD=90°,
∴△ADP∽△OEB,
∴![]() ,
,
∴PD=![]() ,
,
∵AB=2OB,
∴PD=2PF,
∴PF=FD.


科目:初中数学 来源: 题型:
【题目】某巡逻车在一条南北大道上巡逻,某天巡逻车从岗亭A处出发,规定向北方向为正,向南方向为负,当天行驶记录如下(单位:千米) ![]() .
.
(1)最终巡逻车是否回到岗亭![]() 处?若没有,请描述巡逻车的位置:
处?若没有,请描述巡逻车的位置:
(2)若巡逻车行驶1千米耗油0.1升,出发时油箱有油5升,请问途中需要加油吗?若需要,途中至少还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个生产生活现象,可以用“两点之间,线段最短”来解释的是( )
A.用两颗钉子就可以把木条固定在墙上
B.从![]() 地到
地到![]() 地架设电线沿线段
地架设电线沿线段![]() 来架设
来架设
C.植树时定出两棵树的位置后确定同一行树所在的直线
D.打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .
.
(1)![]() 满足何条件时,y随x的增大而减小;
满足何条件时,y随x的增大而减小;
(2)![]() 满足何条件时,图像经过第一、二、四象限;
满足何条件时,图像经过第一、二、四象限;
(3)![]() 满足何条件时,它的图像与y轴的交点在x轴的上方.
满足何条件时,它的图像与y轴的交点在x轴的上方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B.
(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足 时,y1>y2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:第20个“上”字需用多少枚棋子( )

A. 78 B. 82 C. 86 D. 90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决后面两个问题:
一个能被17整除的自然数我们称为“灵动数”.“灵动数”的特征是:若把一个整数的个位数字截去,再从余下的数中,减去个位数的5倍,如果差是17的整倍数(包括0),则原数能被17整除.如果差太大或心算不易看出是否是17的倍数,就继续上述的“截尾、倍大、相减、验差”的过程,直到能清楚判断为止.
例如:判断1675282能不能被17整除. 167528﹣2×5=167518,16751﹣8×5=16711,1671﹣1×5=1666,166﹣6×5=136,到这里如果你仍然观察不出来,就继续…6×5=30,现在个位×5=30>剩下的13,就用大数减去小数,30﹣13=17,17÷17=1;所以1675282能被17整除.
(1)请用上述方法判断7242和2098754 是否是“灵动数”,并说明理由;
(2)已知一个四位整数可表示为![]() ,其中个位上的数字为n,十位上的数字为m,0≤m≤9,0≤n≤9且m,n为整数.若这个数能被51整除,请求出这个数.
,其中个位上的数字为n,十位上的数字为m,0≤m≤9,0≤n≤9且m,n为整数.若这个数能被51整除,请求出这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
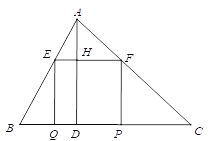
【题目】如图,已知矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD是BC边上的高,AD交EF于H.
(1)求证:![]() ;
;
(2)若BC=10,高AD=8,设EF=x,矩形EFPQ的面积为y,求y与x的函数关系式,并求y的最大值;
(3)若BC=a,高AD=b,直接写出矩形EFPQ的面积的最大值___________.(用a,b表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com