
【题目】已知一次函数![]() .
.
(1)![]() 满足何条件时,y随x的增大而减小;
满足何条件时,y随x的增大而减小;
(2)![]() 满足何条件时,图像经过第一、二、四象限;
满足何条件时,图像经过第一、二、四象限;
(3)![]() 满足何条件时,它的图像与y轴的交点在x轴的上方.
满足何条件时,它的图像与y轴的交点在x轴的上方.
【答案】(1)k>2;(2)2<k<3;(3)k<3且k≠2.
【解析】
(1)根据一次函数的性质,如果y随x的增大而减小,则一次项的系数小于0,由此得出2-k<0,即可求出k的值;
(2)根据一次函数的性质知,当该函数的图象经过第一、二、四象限时,2-k<0,且-2k+6>0,即可求出k的范围;
(3)先求出一次函数y=(2-k)x-2k+6与y轴的交点坐标,再根据图象与y轴的交点在x轴的上方,得出交点的纵坐标大于0,即可求出k的范围.
(1)∵一次函数y=(2k)x2k+6的图象y随x的增大而减小,
∴2k<0,
解得k>2;
(2)∵该函数的图象经过第一、二、四象限,
∴2k<0,且2k+6>0,
解得2<k<3;
(3)∵y=(2k)x2k+6,
∴当x=0时,y=2k+6,
由题意,得2k+6>0且2k≠0,
∴k<3且k≠2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一把直角三角尺的直角顶点放在点
,将一把直角三角尺的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,其中
的下方,其中![]() .
.

(1)将图1中的三角尺绕点![]() 顺时针旋转至图2,使一边
顺时针旋转至图2,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,求
,求![]() 的度数;
的度数;
(2)将图1中三角尺绕点![]() 按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边
按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边![]() 恰好与射线
恰好与射线![]() 平行;在第 秒时,直线
平行;在第 秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() .
.
(3)将图1中的三角尺绕点![]() 顺时针旋转至图3,使
顺时针旋转至图3,使![]() 在
在![]() 的内部,请探究
的内部,请探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家______ 千米,张强从家到体育场用了______ 分钟;
(2)体育场离文具店______ 千米;
(3)张强在文具店逗留了______ 分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,图像与y轴交点在x轴上方?
(3) 若一次函数y=(1-3k)x+2k-1经过点(3,4).请求出一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的新机器可选,其中每台的价格、工作量如下表.
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多2万元,购买2台甲型机器比购买3台乙型机器少6万元.
(1)求a、b的值;
(2)若该公司购买新机器的资金不能超过110万元,请问该公司有几种购买方案?
(3)在(2)的条件下,若公司要求每月的产量不低于2040吨,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了乘法公式![]() 后,老师向同学们提出了如下问题:
后,老师向同学们提出了如下问题:
①将多项式x2+4x+3因式分解;
②求多项式x2+4x+3的最小值.

请你运用上述的方法解决下列问题:
(1)将多项式x2+8x-20因式分解;
(2)求多项式x2+8x-20的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强建设“经济强、环境美、后劲足、群众富”的实力城镇,聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶计划。现决定将A、B两种类型鱼苗共320箱运到某村养殖,其中A种鱼苗比B种鱼苗多80箱。
(1)求A种鱼苗和B种鱼苗各多少箱?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批鱼苗全部运往同一目的地。已知甲种货车最多可装A种鱼苗40箱和B种鱼苗10箱,乙种货车最多可装A种鱼苗和B种鱼苗各20箱。如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元,则安排甲、乙两种货车有哪几种不同的方案?并说明选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
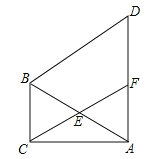
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com