
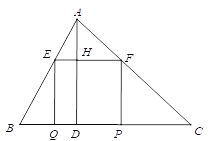
【题目】如图,已知矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD是BC边上的高,AD交EF于H.
(1)求证:![]() ;
;
(2)若BC=10,高AD=8,设EF=x,矩形EFPQ的面积为y,求y与x的函数关系式,并求y的最大值;
(3)若BC=a,高AD=b,直接写出矩形EFPQ的面积的最大值___________.(用a,b表示)
【答案】(1)见解析;(2)y=![]() ,20;(3)
,20;(3)![]() .
.
【解析】(1)由EF∥BC,得到△AEF∽△ABC,由相似三角形对应高之比等于相似比即可得到结论;
(2)由(1)的结论,求出AH、HD的长,由EFPQ的面积=EF×HD即可得到结论;
(3)类似(2)可得到结论.
(1)∵四边形EFPQ是矩形,∴EF∥BC,∴△AEF∽△ABC,∴![]() ;
;
(2)由(1)得:![]() ,∴
,∴![]() ,∴AH=0.8x,∴HD=AD-AH=8-0.8x,∴y=EFPQ的面积=EF×HD=x(8-0.8x)=
,∴AH=0.8x,∴HD=AD-AH=8-0.8x,∴y=EFPQ的面积=EF×HD=x(8-0.8x)=![]() ,∴当x=5时,y的最大值为20.
,∴当x=5时,y的最大值为20.
(3)∵![]() ,∴
,∴![]() ,∴AH=
,∴AH=![]() ,∴矩形EFPQ的面积=EF×HD=
,∴矩形EFPQ的面积=EF×HD=![]() =
=![]() ,∴矩形EFPQ的面积的最大值为
,∴矩形EFPQ的面积的最大值为![]() .
.


科目:初中数学 来源: 题型:
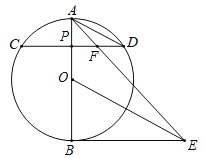
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
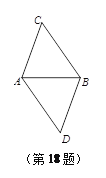
【题目】如图,将线段AB绕点A逆时针旋转α度角得到线段AC,将线段AB绕点B逆时针旋转α度角得到线段BD(0°<α<180°),连结BC、AD.当α=_______度时,四边形ACBD是菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1) A商品的单价是___________元,B商品的单价是___________元;
(2) 已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,设购买A商品的件数为x件,该商店购买的A、B两种商品的总费用为y元.
① 求y与x的函数关系式.
② 如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,求购买B商品最多有多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,然后回答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,所以
是无理数,而无理数是无限不循环小数,所以![]() 的小数部分我们不可能全部写出来,由于
的小数部分我们不可能全部写出来,由于![]() 的整数部分是1,将
的整数部分是1,将![]() 减去它的整数部分,差就是它的小数部分,因此
减去它的整数部分,差就是它的小数部分,因此![]() 的小数部分可用
的小数部分可用![]() ﹣1表示.
﹣1表示.
由此我们得到一个真命题:如果![]() =x+y,其中x是整数,且0<y<1,那么x=1,y=
=x+y,其中x是整数,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
请解答下列问题:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= ,b= ;
=a+b,其中a是整数,且0<b<1,那么a= ,b= ;
(2)如果﹣![]() =c+d,其中c是整数,且0<d<1,那么c= ,d= ;
=c+d,其中c是整数,且0<d<1,那么c= ,d= ;
(3)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
![]()
(1)若表示1的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示 的点重合;
的点与表示 的点重合;
(2)若表示![]() 的点与表示3的点重合,回答以下问题:
的点与表示3的点重合,回答以下问题:
①表示5的点与表示 的点重合:
②若数轴上![]() 、
、![]() 两点之间的距离为14(
两点之间的距离为14(![]() 在
在![]() 的左侧),且
的左侧),且![]() 、
、![]() 两点经折叠后重合,求
两点经折叠后重合,求![]() 、
、![]() 两点表示的数是多少?
两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c是△ABC的三条边,关于x的方程x2+2![]() x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
(1)求证:△ABC为等边三角形;
(2)若a,b为方程x2+mx-3m=0的两根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形 ABCD 中,AD∥BC,E 是 AB 的中点,CE 的延长线与 DA 的延长线相 交于点 F.
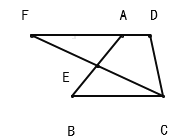
(1)求证:△BCE≌△AFE;
(2)连接 AC、FB,则 AC 与 FB 的数量关系是 ,位置关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com