
【题目】已知:如图,在梯形 ABCD 中,AD∥BC,E 是 AB 的中点,CE 的延长线与 DA 的延长线相 交于点 F.
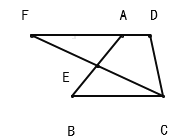
(1)求证:△BCE≌△AFE;
(2)连接 AC、FB,则 AC 与 FB 的数量关系是 ,位置关系是 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
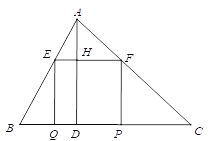
【题目】如图,已知矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD是BC边上的高,AD交EF于H.
(1)求证:![]() ;
;
(2)若BC=10,高AD=8,设EF=x,矩形EFPQ的面积为y,求y与x的函数关系式,并求y的最大值;
(3)若BC=a,高AD=b,直接写出矩形EFPQ的面积的最大值___________.(用a,b表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问:
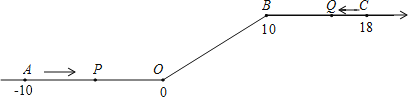
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.

(1)当OC旋转10秒时,∠COD= °.
(2)当旋转时间为 秒时,OC与OD的夹角是30°.
(3)当旋转时间为 秒时,OB平分∠COD时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售甲,乙两种型号的新能源汽车,上周售出甲型汽车和乙型汽车各2辆,销售额为88万元;本周售出3辆甲型汽车和1辆乙型汽车,两周的销售额为184万元.
(1)求每辆甲型汽车和乙型汽车的售价;
(2)某公司拟向该店购买甲,乙两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com