
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ��10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮�ʣ�
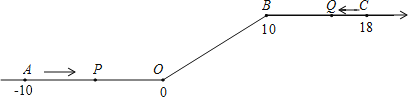
��1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
���𰸡���1��19�룻��2��![]() ����3��t��ֵΪ2��6.5��11��17
����3��t��ֵΪ2��6.5��11��17
��������
��1������·�̳����ٶȵ���ʱ�䣬�ɵô𰸣�
��2����������ʱP��Q��ʱ����ȣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��3������PO��BQ��ʱ����ȣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
�⣺��1����P�˶�����Cʱ������ʱ��t��10��2+10��1+8��2��19���룩��
��2�������֪��P��Q�����������߶�OB����M������OM��x��
��10��2+x��1��8��1+��10��x����2��
���x��![]() ��
��
��������M����Ӧ������![]() ��
��
��3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ�
�ٶ���Q��CB�ϣ�����P��AO�ϣ���8��t��10��2t����ã�t��2��
�ڶ���Q��CB�ϣ�����P��OB�ϣ���8��t����t��5����1����ã�t��6.5��
�۶���Q��BO�ϣ�����P��OB�ϣ���2��t��8������t��5����1����ã�t��11��
�ܶ���Q��OA�ϣ�����P��BC�ϣ���10+2��t��15����t��13+10����ã�t��17��
����������t��ֵΪ2��6.5��11��17��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��y��x�IJ��ֶ�Ӧֵ���±���
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
���н��ۣ��������ߵĿ������£�����ͼ��ĶԳ���Ϊx=1;�۵�x��lʱ������ֵy��x ����������ܷ���ax2+bx+c=0��һ��������4.������ȷ�Ľ����У� ��
A. 4��B. 1��C. 3��D. 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
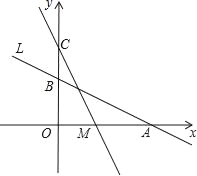
����Ŀ����ͼ��ֱ��L��y=-![]() x+2��x�ᡢy��ֱ���A��B���㣬��y������һ��C��0��4��������M��A����ÿ��1����λ���ٶ���x�������ƶ���
x+2��x�ᡢy��ֱ���A��B���㣬��y������һ��C��0��4��������M��A����ÿ��1����λ���ٶ���x�������ƶ���
��1����A��B��������ꣻ
��2������COM�����S��M���ƶ�ʱ��t֮��ĺ�����ϵʽ��
��3����tΪ��ֵʱ��COM�ա�AOB�������ʱM������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������O�ں��й����У����ֵ���A������ƫ��60��ķ����ϣ�ͬʱ��������ƫ��30�㡢����������ƫ��45�㣩�������ֱַ����˿���B�ͺ���C��
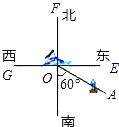
��1�����ձ�ʾ������λ�ķ������ֱ���ʾ����B�ͺ���C���������OB��OC����д��������
��2����ͼ����һ���洬D���ҡ�AOD�IJ�����������ǵ�3���������AOD�Ķ�����
��3��������ʾ�洬D���������OD�����洬D�ڻ���O���� ��д����λ�ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8�֣�
��ͼ����E��F��BC�ϣ�BE��CF����A����D����B����C��AF��DE���ڵ�O��

(1)��֤��AB��DC��
(2)���ж���OEF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����30����ֱ�����dz�ABC��ֱ�Ƕ���A��ʱ����ת��ADE��λ�ã�ʹB��Ķ�Ӧ��D����BC���ϣ�����EB��EC�������н��ۣ��١�DAC=��DCA����EDΪAC�Ĵ�ֱƽ���ߣ��ۡ�BED=30�㣻��ED=2AB��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
��1��![]() ��
��
��2��![]() ��
��
��3��![]() ��
��
��4��![]() ��
��
����
����������ʽ�Ĺ��ɣ�����������⣺
��1��д����5����ʽ��________________��
��2��д����![]() ����ʽ��__________________���ú���
����ʽ��__________________���ú���![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��3��Ӧ���㷢�ֵĹ��ɣ����㣺![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�У�BF��AC�������ߣ���D��BF�ϣ�����AD����AD���Ҳ����ȱߡ�ADE������EF������AEF�ܳ���Сʱ����CFE�Ĵ�С�ǣ�������

A. 30�� B. 45�� C. 60�� D. 90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABC�ڽ�����O������O�İ뾶Ϊ6��sinA=![]() ����BC�ij���
����BC�ij���

���𰸡�BC=8��
�����������������ͨ���������߹���ֱ�������Σ����������Ǻ���֪ʶ������⣮
�������������O��ֱ��CD������BD����CD=2��6=12.
��![]()
��![]()
��![]()

�㾦��ֱ�����Ե�Բ�ܽ���ֱ��.
�����͡������
��������
22
����Ŀ����ͼ��һ�κ���y=k1x+b�뷴��������y=![]() ��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽk1x+b��![]() �Ľ⼯��
�Ľ⼯��
��3����P��p��y1����Q����2��y2���Ǻ���y=![]() ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��
ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com