
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
【答案】D
【解析】分析:首先证明点E在射线CE上运动(∠ACE=30°),
因为AF为定值,所以当AE+EF最小时,△AEF的周长最小,
作点A关于直线CE的对称点M,连接FM交CE 于E′,此时AE′+FE′的值最小,
根据等边三角形的判定和性质即可求出∠CFE的大小.
详解:∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠ABC=60°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE,
∴∠ABD=∠ACE,
∵AF=CF,
∴∠ABD=∠CBD=∠ACE=30°,
∴点E在射线CE上运动(∠ACE=30°),
作点A关于直线CE的对称点M,连接FM交CE 于E′,此时AE′+FE′的值最小,
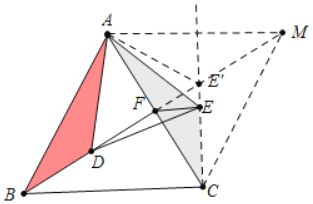
∵CA=CM,∠ACM=60°,
∴△ACM是等边三角形,
∵AF=CF,
∴FM⊥AC,
∴∠CFE′=90°,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问:
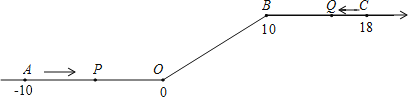
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
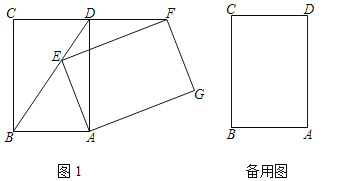
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-3-7;
(2) ![]() ;
;
(3)-0.5+(-15.5)-(-17)-|-12|;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() (用简便方法计算).
(用简便方法计算).
查看答案和解析>>
科目:初中数学 来源: 题型:
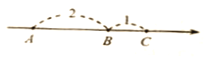
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示. 设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数为 、 ,p的值为 ;若以C为原点,p 的值为 ;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
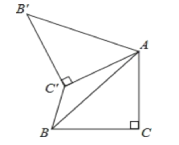
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为_________.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的定价是每千克5元,元旦期间,该商品推出优惠活动,若一次购买该商品的数量超过2千克,则超过2千克的部分,价格打8折;若一次购买的数量不超过2千克(含2千克),仍按原价付款
(1)根据题意,填写下表
购买的数量(千克) | 1.5 | 2 | 3.5 | 4 | … |
付款金额(元) | 7.5 | 16 | … |
(2)若一次购买的数量为![]() 千克,请你写出付款金额
千克,请你写出付款金额![]() (元)与
(元)与![]() (千克)之间的关系式
(千克)之间的关系式
(3)若某顾客一次购买该商品花费了68元,求该顾客购买商品的数量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com