
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为_________.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为_________.
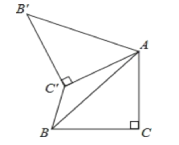
【答案】![]()
【解析】
连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD-C′D计算即可得解.
如图,连接BB′,
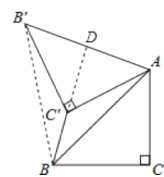
∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,
∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴AB=BB′,
在△ABC′和△B′BC′中,
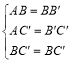 ,
,
∴△ABC′≌△B′BC′(SSS),
∴∠ABC′=∠B′BC′,
延长BC′交AB′于D,
则BD⊥AB′,
∵∠C=90°,AC=BC=![]() ,
,
∴AB=![]() ,
,
∴BD=2×![]() =
=![]() ,
,
C′D=![]() ×2=1,
×2=1,
∴BC′=BDC′D=![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
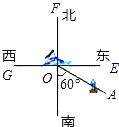
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB、OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,求出∠AOD的度数;
(3)画出表示渔船D方向的射线OD,则渔船D在货轮O的 (写出方位角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,以A为圆心,AB为半径的圆交AD于F,交BC于G,延长BA交圆于E.
(1)若ED与⊙A相切,试判断GD与⊙A的位置关系,并证明你的结论;
(2)在(1)的条件不变的情况下,若GC=CD,求∠C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索代数式a2![]() 2ab+b2与代数式(a
2ab+b2与代数式(a ![]() b)2的关系.
b)2的关系.
(1)当a=1,b=2时分别计算两个代数式的值.
(2)当a=3,b= ![]() 2时分别计算两个代数式的值.
2时分别计算两个代数式的值.
(3)你发现了什么规律?
(4)利用你发现的规律计算:732![]() 2×73×67+672.
2×73×67+672.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(![]() ,0),点B(0,1),直线EF与x轴垂直,A为垂足。
,0),点B(0,1),直线EF与x轴垂直,A为垂足。
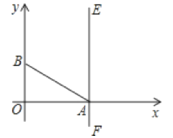
(1)若线段AB绕点A按顺时针方向旋转到AB′的位置,并使得AB与AB′关于直线EF对称,请你画出线段AB所扫过的区域(用阴影表示);
(2)计算(1)中线段AB所扫过区域的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,在△ABC内部作△CED,使∠CED=90°,E在BC上,D在AC上,分别以AB,AD为邻边作平行四边形ABFD,连接AF、AE、EF.
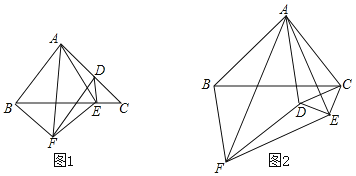
(1)证明:AE=EF;
(2)判断线段AF,AE的数量关系,并证明你的结论;
(3)在图(1)的基础上,将△CED绕点C逆时针旋转,请判断(2)问中的结论是否成立?若成立,结合图(2)写出证明过程;若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com