Question

【题目】如图，已知∠AOB=90°，射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1°的速度逆时针方向旋转．当OC与OA成180°时，OC与OD同时停止旋转．

（1）当OC旋转10秒时，∠COD=　 　°．

（2）当旋转时间为　 　秒时，OC与OD的夹角是30°．

（3）当旋转时间为　 　秒时，OB平分∠COD时．

Answer 1

【答案】（1）∠COD=40°；（2）12或24；（3）30.

【解析】试题分析：（1）根据旋转的速度和旋转的时间分别求出∠AOC和∠BOD的度数，然后根据∠COD＝∠AOB－∠AOC－∠BOD即可计算得出结论；

（2）设转动t秒，OC与OD的夹角是30度，①如图1，列方程即可得到结论；②如图2，列方程即可得到结论；

（3）如图3，设转动m秒时，根据角平分线的定义列方程即可得到结论．

试题解析：

解：（1）∵射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转，

∴当OC旋转10秒时，∠COD＝∠AOB-4°×10-1°×10＝40°，

故答案为：40；

（2）设转动t秒，OC与OD的夹角是30度，

①如图1，4t＋t＝90－30，

t＝12，

②如图2，4t＋t＝90＋30，

t＝24，

∴旋转的时间是12秒或24秒，

故答案为12或24；

（3）如图3，设转动m秒时，OB平分∠COD，

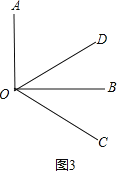
则4m－90＝m，

解得，m＝30，

∴旋转的时间是30秒，

故答案为30．