
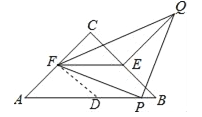
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
【答案】D
【解析】解:连结FD,D是AB的中点,如图.∵△ABC为等腰直角三角形,AB=10,PB=1,∴AC=BC=![]() ,∠A=45°.∵点D、E、F分别是△ABC三边的中点,AB=10,PB=1,∴AD=BD= 5,DP=DB﹣PB=5﹣1=4,EF、DF为△ABC的中位线,∴EF∥AB,EF=
,∠A=45°.∵点D、E、F分别是△ABC三边的中点,AB=10,PB=1,∴AD=BD= 5,DP=DB﹣PB=5﹣1=4,EF、DF为△ABC的中位线,∴EF∥AB,EF= ![]() AB=5,DF=
AB=5,DF= ![]() BC=
BC=![]() ,∠EFP=∠FPD,∴∠FDA=45°,
,∠EFP=∠FPD,∴∠FDA=45°,![]() =
=![]() =
=![]() ,∴∠DFP+∠DPF=45°.∵△PQF为等腰直角三角形,∴∠PFE+∠EFQ=45°,FP=PQ,∴∠DFP=∠EFQ.∵△PFQ是等腰直角三角形,∴
,∴∠DFP+∠DPF=45°.∵△PQF为等腰直角三角形,∴∠PFE+∠EFQ=45°,FP=PQ,∴∠DFP=∠EFQ.∵△PFQ是等腰直角三角形,∴![]() =
= ![]() ,∴
,∴![]() =
= ![]() ,∴△FDP∽△FEQ,∴
,∴△FDP∽△FEQ,∴![]() =
=![]() ,∴QE=
,∴QE= ![]() DP=
DP=![]() .故选D.
.故选D.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为﹣3,点B表示的数为3,若在数轴上存在点P,使得AP+BP=m,则称点P为点A和B的“m级精致点”,例如,原点O表示的数为0,则AO+BO=3+3=6,则称点O为点A和点B的“6级精致点”,根据上述规定,解答下列问题:
(1)若点C轴在数轴上表示的数为﹣5,点C为点A和点B的“m级精致点”,则m= ;
(2)若点D是数轴上点A和点B的“8级精致点”,求点D表示的数;
(3)如图,数轴上点E和点F分别表示的数是﹣2和4,若点G是点E和点F的“m级精致点”,且满足GE=3GF,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是![]() ,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
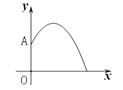
A. 1个 B. 2个 C. 3个 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
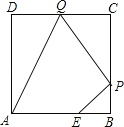
A. 3 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知单位长度为1的方格中有三角形ABC.
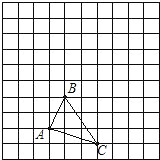
(1)请画出三角形ABC向上平移3格再向右平移2格后所得到的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标;
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若a,b互为相反数,则![]() =-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为
=-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为![]() 分.其中正确的为____(填序号).
分.其中正确的为____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)证明:无论m为何值方程都有两个实数根;
(2)是否存在正数m,使方程的两个实数根的平方和等于26?若存在,求出满足条件的正数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
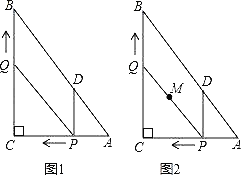
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数28、29.4、31.9、27、28.8、34.1、29.4的中位数、众数、极差分别是( )
A. ![]() 、
、![]() 、
、![]() B.
B. ![]() 、
、![]() 、
、![]()
C. 27、29、![]() D.
D. ![]() 、28、
、28、![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com