
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④当﹣1<x<3时,y>0;其中正确的是( )
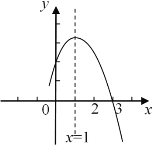
A.①②B.①②④C.②③④D.③④
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
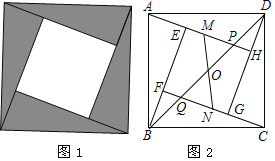
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AB=10,BC=16,cosB=![]() ,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
(1)当圆C经过点A时,求CP的长
(2)联结AP,当AP//CG时,求弦EF的长
(3)当△AGE是等腰三角形时,求圆C的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(2,1),B(1,4),C(3,2).请解答下列问题:
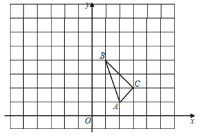
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的右侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点的坐标;
(3)如果点D(a,b)在线段BC上,请直接写出经过(2)的变化后对应点D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求8名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
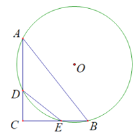
【题目】如图,在△ABC中,tan∠BAC![]() tan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
tan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
A.![]() B.
B.![]()
C.13D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com