
【题目】如图,已知在平行四边形ABCD中,AB=10,BC=16,cosB=![]() ,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
(1)当圆C经过点A时,求CP的长
(2)联结AP,当AP//CG时,求弦EF的长
(3)当△AGE是等腰三角形时,求圆C的半径长.

【答案】(1)10;(2)![]() ;(3)
;(3)![]()
【解析】
(1)当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,根据![]() ,求出BH的长度,得出AH垂直平分BC,由垂直平分线的性质得到AB=AC,从而得到CP=AC即可;
,求出BH的长度,得出AH垂直平分BC,由垂直平分线的性质得到AB=AC,从而得到CP=AC即可;
(2)首先得出四边形APCE是菱形,进而得出CN的长,进而利用锐角三角函数关系得出CP,再由勾股定理及垂径定理求出EF的长;
(3)∠GAE≠∠BGC,只能∠AGE=∠AEG,利用AD∥BC,得出△GAE∽△GBC,列出相似比解出AE=6,从而得出EN的值,再由勾股定理即可求出CE的值.
解:(1)过点A作AH⊥BC,垂足为H,联结AC.
在Rt△AHB中,∠AHB=90°,![]()
∵AB=10,
∴BH=8,AH=![]()
∵BC=16,
∴AH垂直平分BC,
∴AB=AC=10,
∵圆C经过点A,
∴CP=AC=10,
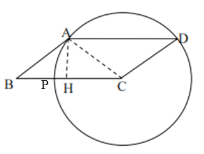
(2)过点C作CM⊥AD,垂足为M,
∵四边形ABCD是平行四边形,
AD∥BC,
若AP//CG,
则四边形APCE为平行四边形,
∵CE=CP,
∴平行四边形APCE是菱形,
连接AC,PE交于点N,则AC⊥PE,
∴AN=CN=![]() ,
,
由(1)可知AC=AB=10,CM=AH=6
∴AN=CN=5,∠ABC=∠ACB,
∴CP=CE=![]() ,
,
则EF=2EM=![]() ,
,
∴当AP∥CG时,弦EF的长为![]() .
.
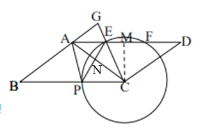
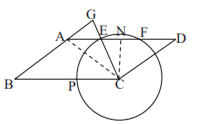
(3)∵![]() ,
,
∴∠B﹤45°,
又∵∠BCG﹤90°,
∴∠BGC﹥45°,
又∵∠AEG=∠BCG≥∠ACB=∠B,
∴当∠AEG=∠B时,A、E、G重合,
只能∠AGE=∠AEG,
∵AD∥BC,
∴△GAE∽△GBC
∴![]() ,即
,即![]() ,解得
,解得![]()
∴EN=AN-AE=2,
∴![]() .
.
∴圆C的半径长为![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
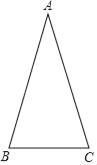
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
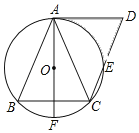
【题目】如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (b,c为常数).
(b,c为常数).
(1)若抛物线的顶点坐标为(1,1),求b,c的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围;
(3)在(1)的条件下,存在正实数m,n( m<n),当m≤x≤n时,恰好有![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学习兴趣如何是每位教师非常关注的问题.为此,某校教师对该校部分学生的学习兴趣进行了一次抽样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣;B层次:较感兴趣;C层次:不感兴趣);并将调查结果绘制成了图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
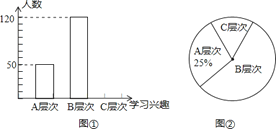
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求图②中C层次所在扇形的圆心角的度数;
(4)根据抽样调查的结果,请你估计该校1200名学生中大约有多少名学生对学习感兴趣(包括A层次和B层次).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④当﹣1<x<3时,y>0;其中正确的是( )
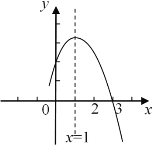
A.①②B.①②④C.②③④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
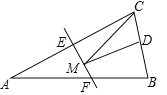
【题目】如图,等腰![]() 的底边
的底边![]() 长为4,面积为12,腰
长为4,面积为12,腰![]() 的垂直平分线
的垂直平分线![]() 分别交边
分别交边![]() 于点
于点![]() ,若点D是的
,若点D是的![]() 中点,点M为线段
中点,点M为线段![]() 上一动点,当
上一动点,当![]() 的周长最小时,
的周长最小时,![]() 长为( )
长为( )
A.1B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:将正m边形(m≥3)不断向外扩展,每扩展一个正m边形每条边上的点的个数(以下简称“点数”)就增加一个,则n个正m边形的点数总共有多少个?
问题探究:为了解决上面的问题,我们将采取将一般问题特殊化的策略,先从简单和具体的情形入手:
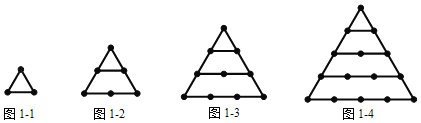
探究一:n个正三角形的点数总共有多少个?
如图1﹣1,1个正三角形的点数总共有3个;如图1﹣2,2个正三角形的点数总共有6个;如图1﹣3,3个正三角形的点数总共有10个;…;n个正三角形的点数总共有 个.
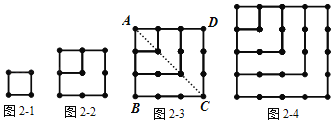
探究二:n个正四边形的点数总共有多少个?
如图2﹣1,1个正四边形的点数总共有4个;如图2﹣2,2个正四边形的点数总共有9个;
如图2﹣3,连接AC,得到两个三角形△ABC和△ADC,这两个三角形相同之处在于,BC边与CD边都有相同个数的点,即4个点,并且与BC、CD平行的边上依次减少一个点直至顶点A,每个三角形都有10个点,两个三角形就是2×10个点.因为这两个三角形在AC上有4个点重合,所以3个正四边形的点数总共有2×10﹣4=16(个).
如图2﹣4,4个正四边形的点数总共有 个;……n个正四边形的点数总共有 个.
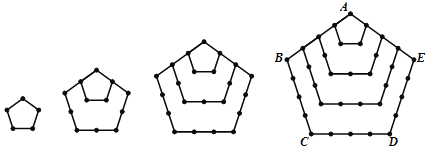
探究三:n个正五边形的点数总共有多少个?
类比探究二的方法,求4个正五边形的点数总共有多少个?并叙述你的探究过程.
n个正五边形的点数总共有 个.
探究四:n个正六边形的点数总共有 个.
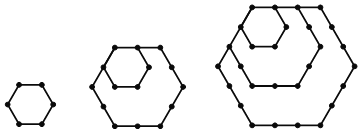
问题解决:n个正m边形的点数总共有 个.
实际应用:若99个正m边形的点数总共有39700个,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com