
ЁОЬтФПЁПЮЪЬтЬсГіЃКНЋе§mБпаЮ(mЁн3)ВЛЖЯЯђЭтРЉеЙЃЌУПРЉеЙвЛИіе§mБпаЮУПЬѕБпЩЯЕФЕуЕФИіЪ§(вдЯТМђГЦЁАЕуЪ§ЁБ)ОЭдіМгвЛИіЃЌдђnИіе§mБпаЮЕФЕуЪ§змЙВгаЖрЩйИіЃП
ЮЪЬтЬНОПЃКЮЊСЫНтОіЩЯУцЕФЮЪЬтЃЌЮвУЧНЋВЩШЁНЋвЛАуЮЪЬтЬиЪтЛЏЕФВпТдЃЌЯШДгМђЕЅКЭОпЬхЕФЧщаЮШыЪжЃК
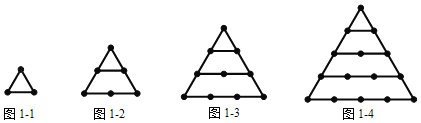
ЬНОПвЛЃКnИіе§Ш§НЧаЮЕФЕуЪ§змЙВгаЖрЩйИіЃП
ШчЭМ1Љ1ЃЌ1Иіе§Ш§НЧаЮЕФЕуЪ§змЙВга3ИіЃЛШчЭМ1Љ2ЃЌ2Иіе§Ш§НЧаЮЕФЕуЪ§змЙВга6ИіЃЛШчЭМ1Љ3ЃЌ3Иіе§Ш§НЧаЮЕФЕуЪ§змЙВга10ИіЃЛЁЃЛnИіе§Ш§НЧаЮЕФЕуЪ§змЙВгаЁЁ ЁЁИіЃЎ
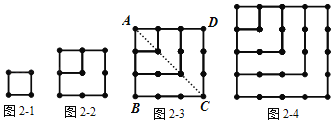
ЬНОПЖўЃКnИіе§ЫФБпаЮЕФЕуЪ§змЙВгаЖрЩйИіЃП
ШчЭМ2Љ1ЃЌ1Иіе§ЫФБпаЮЕФЕуЪ§змЙВга4ИіЃЛШчЭМ2Љ2ЃЌ2Иіе§ЫФБпаЮЕФЕуЪ§змЙВга9ИіЃЛ
ШчЭМ2Љ3ЃЌСЌНгACЃЌЕУЕНСНИіШ§НЧаЮЁїABCКЭЁїADCЃЌетСНИіШ§НЧаЮЯрЭЌжЎДІдкгкЃЌBCБпгыCDБпЖМгаЯрЭЌИіЪ§ЕФЕуЃЌМД4ИіЕуЃЌВЂЧвгыBCЁЂCDЦНааЕФБпЩЯвРДЮМѕЩйвЛИіЕужБжСЖЅЕуAЃЌУПИіШ§НЧаЮЖМга10ИіЕуЃЌСНИіШ§НЧаЮОЭЪЧ2ЁС10ИіЕуЃЎвђЮЊетСНИіШ§НЧаЮдкACЩЯга4ИіЕужиКЯЃЌЫљвд3Иіе§ЫФБпаЮЕФЕуЪ§змЙВга2ЁС10Љ4ЃН16(Иі)ЃЎ
ШчЭМ2Љ4ЃЌ4Иіе§ЫФБпаЮЕФЕуЪ§змЙВгаЁЁ ЁЁИіЃЛЁЁnИіе§ЫФБпаЮЕФЕуЪ§змЙВгаЁЁ ЁЁИіЃЎ
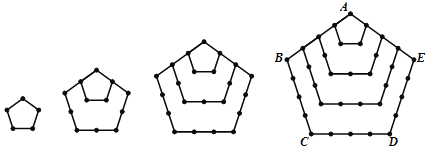
ЬНОПШ§ЃКnИіе§ЮхБпаЮЕФЕуЪ§змЙВгаЖрЩйИіЃП
РрБШЬНОПЖўЕФЗНЗЈЃЌЧѓ4Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЖрЩйИіЃПВЂа№ЪіФуЕФЬНОПЙ§ГЬЃЎ
nИіе§ЮхБпаЮЕФЕуЪ§змЙВгаЁЁ ЁЁИіЃЎ
ЬНОПЫФЃКnИіе§СљБпаЮЕФЕуЪ§змЙВгаЁЁ ЁЁИіЃЎ
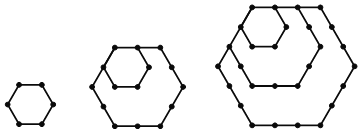
ЮЪЬтНтОіЃКnИіе§mБпаЮЕФЕуЪ§змЙВгаЁЁ ЁЁИіЃЎ
ЪЕМЪгІгУЃКШє99Иіе§mБпаЮЕФЕуЪ§змЙВга39700ИіЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЬНОПвЛЃК![]() ЃЛЬНОПЖўЃК25ЃЌ(n+1)2ЃЛЬНОПШ§ЃК
ЃЛЬНОПЖўЃК25ЃЌ(n+1)2ЃЛЬНОПШ§ЃК![]() (n+1)(3n+2)ЃЛЬНОПЫФЃК(n+1)(2n+1)ЃЛЮЪЬтНтОіЃК
(n+1)(3n+2)ЃЛЬНОПЫФЃК(n+1)(2n+1)ЃЛЮЪЬтНтОіЃК![]() ЃЛЪЕМЪгІгУЃКm=10
ЃЛЪЕМЪгІгУЃКm=10
ЁОНтЮіЁП
ЬНОПвЛЃКnИіе§Ш§НЧаЮЕФЕуЪ§змИіЪ§ЪЧЧА(n+1)ИіЪ§ЕФКЭЃЛ
ЬНОПЖўЃК4ЃЌ9ЃЌ16ЃЌ25ЁЃЌЗЂЯжnИіе§ЫФБпаЮЕФЕуЪ§змЙВга(n+1)2ИіЃЛ
ЬНОПШ§ЃКШчЭМ3Љ1ЃЌжБНгЪ§ЕуЕФИіЪ§ЮЊ5ИіЃЌШчЭМ3Љ2ЃЌСЌНгACЃЌADЃЌЕУЕНШ§ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга6ИіЕуЃЌОЭЪЧ3ЁС6ЃН18ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга3ИіЕужиКЯЃЌЫљвдЃЌ2Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК3ЁС6Љ2ЁС3ЃН12ИіЃЛЭЌРэЕУШчЭМ3Љ3ЃЌ3Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК3ЁС10Љ2ЁС4ЃН22ИіЃЛШчЭМ3Љ4ЃЌ4Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК3ЁС15Љ2ЁС5ЃН35ИіЃЌШЗЖЈЙцТЩЕУЃКnИіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК![]() ИіЃЛ
ИіЃЛ
ЬНОПЫФЃКШчЭМ3Љ1ЃЌжБНгЪ§ЕуЕФИіЪ§ЮЊ6ИіЃЌШчЭМ4Љ2ЃЌСЌНгA'C'ЃЌA'D'ЃЌA'E'ЃЌЕУЕН4ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга1+2+3ЃН6ИіЕуЃЌОЭЪЧ24ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга3ИіЕужиКЯЃЌЫљвдЃЌ2Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК4ЁС6Љ3ЁС3ЃН15ИіЃЛЭЌРэЕУЕуЕФИіЪ§вРДЮЮЊЃК28ЃЌ45ЃН5ЁС9ЃЌЁЃЌ(n+1)(2n+1)ИіЃЛ
ЮЪЬтНтОіЃКИљОнвдЩЯЙцТЩПЩЕУНсТлЃЛ
ЪЕМЪгІгУЃКНЋnЃН99ДњШыЮЪЬтНтОіЕФЕШЪНжаНтЗНГЬМДПЩЃЎ
НтЃКЬНОПвЛЃК
ШчЭМ1Љ1ЃЌ1Иіе§Ш§НЧаЮЕФЕуЪ§змЙВга3ИіЃЌМД3ЃН1+2ЃЛ
ШчЭМ1Љ2ЃЌ2Иіе§Ш§НЧаЮЕФЕуЪ§змЙВга6ИіЃЌМД6ЃН1+2+3ЃЛ
ШчЭМ1Љ3ЃЌ3Иіе§Ш§НЧаЮЕФЕуЪ§змЙВга10ИіЃЌМД10ЃН1+2+3+4ЃЛ
ЁЃЛ
nИіе§Ш§НЧаЮЕФЕуЪ§змЙВгаЃК![]() ИіЃЛ
ИіЃЛ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЬНОПЖўЃК
ШчЭМ2Љ1ЃЌ1Иіе§ЫФБпаЮЕФЕуЪ§змЙВга4ИіЃЌМД4ЃН22ЃЛ
ШчЭМ2Љ2ЃЌ2Иіе§ЫФБпаЮЕФЕуЪ§змЙВга9ИіЃЌМД9ЃН32ЃЛ
ШчЭМ2Љ3ЃЌСЌНгACЃЌЕУЕНСНИіШ§НЧаЮЁїABCКЭЁїADCЃЌетСНИіШ§НЧаЮЯрЭЌжЎДІдкгкЃЌBCБпгыCDБпЖМгаЯрЭЌИіЪ§ЕФЕуЃЌМД4ИіЕуЃЌВЂЧвгыBCЁЂCDЦНааЕФБпЩЯвРДЮМѕЩйвЛИіЕужБжСЖЅЕуAЃЌУПИіШ§НЧаЮЖМга10ИіЕуЃЌСНИіШ§НЧаЮОЭЪЧ2ЁС10ИіЕуЃЎвђЮЊетСНИіШ§НЧаЮдкACЩЯга4ИіЕужиКЯЃЌЫљвд3Иіе§ЫФБпаЮЕФЕуЪ§змЙВга2ЁС10Љ4ЃН16(Иі)ЃЌМД16ЃН42ЃЛ
ШчЭМ2Љ4ЃЌСЌНгACЃЌЕУЕНСНИіШ§НЧаЮЁїABCКЭЁїADCЃЌетСНИіШ§НЧаЮЯрЭЌжЎДІдкгкЃЌBCБпгыCDБпЖМгаЯрЭЌИіЪ§ЕФЕуЃЌМД5ИіЕуЃЌВЂЧвгыBCЁЂCDЦНааЕФБпЩЯвРДЮМѕЩйвЛИіЕужБжСЖЅЕуAЃЌУПИіШ§НЧаЮЖМга15ИіЕуЃЌСНИіШ§НЧаЮОЭЪЧ2ЁС15ИіЕуЃЎвђЮЊетСНИіШ§НЧаЮдкACЩЯга5ИіЕужиКЯЃЌЫљвд4Иіе§ЫФБпаЮЕФЕуЪ§змЙВга2ЁС15Љ5ЃН25(Иі)ЃЌМД25ЃН52ЃЛ
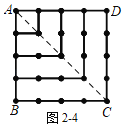
ЁрnИіе§ЫФБпаЮЕФЕуЪ§змЙВга![]() ИіЃЛ
ИіЃЛ
ЙЪД№АИЮЊЃК25ЃЌ(n+1)2ЃЛ
ЬНОПШ§ЃК
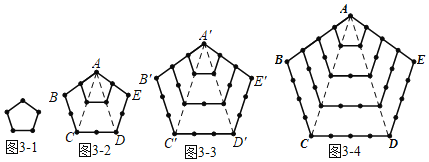
ШчЭМ3Љ1ЃЌ1Иіе§ЮхБпаЮЕФЕуЪ§змЙВга5ИіЃЌМД![]() ЃЛ
ЃЛ
ШчЭМ3Љ2ЃЌСЌНгACЃЌADЃЌЕУЕНШ§ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга6ИіЕуЃЌОЭЪЧ3ЁС6ЃН18ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга3ИіЕужиКЯЃЌЫљвдЃЌ2Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК3ЁС6Љ2ЁС3ЃН12ИіЃЌМД![]() ЃЛ
ЃЛ
ШчЭМ3Љ3ЃЌСЌНгA'C'ЃЌA'D'ЃЌЕУЕНШ§ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга10ИіЕуЃЌОЭЪЧ3ЁС10ЃН30ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга4ИіЕужиКЯЃЌЫљвдЃЌ3Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК3ЁС10Љ2ЁС4ЃН22ИіЃЌМД![]() ЃЛ
ЃЛ
ШчЭМ3Љ4ЃЌСЌНгACЃЌADЃЌЕУЕНШ§ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга15ИіЕуЃЌОЭЪЧ3ЁС15ЃН45ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга5ИіЕужиКЯЃЌЫљвдЃЌ4Иіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК3ЁС15Љ2ЁС5ЃН35ИіЃЌМД![]() ЃЛ
ЃЛ
Ё
ЭЌРэЕУЃКnИіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК![]() (n+1)(3n+2)ИіЃЛ
(n+1)(3n+2)ИіЃЛ
ЙЪД№АИЮЊЃК![]() (n+1)(3n+2)ЃЛ
(n+1)(3n+2)ЃЛ
ЬНОПЫФЃК
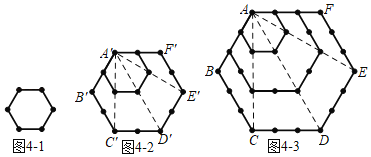
ШчЭМ4Љ1ЃЌ1Иіе§СљБпаЮЕФЕуЪ§змЙВга6ИіЃЌМД6ЃН2ЁС3ЃЛ
ШчЭМ4Љ2ЃЌСЌНгA'C'ЃЌA'D'ЃЌA'E'ЃЌЕУЕН4ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга6ИіЕуЃЌОЭЪЧ4ЁС6ЃН24ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга3ИіЕужиКЯЃЌЫљвдЃЌ2Иіе§СљБпаЮЕФЕуЪ§змЙВгаЃК4ЁС6Љ3ЁС3ЃН15ИіЃЌМД15ЃН3ЁС5ЃЛ
ШчЭМ4Љ3ЃЌСЌНгACЃЌADЃЌAEЃЌЕУЕН4ИіШ§НЧаЮЃЌУПИіШ§НЧаЮЖМга10ИіЕуЃЌОЭЪЧ4ЁС10ЃН40ИіЕуЃЌвђЮЊУПСНИіШ§НЧаЮга4ИіЕужиКЯЃЌЫљвдЃЌ3Иіе§СљБпаЮЕФЕуЪ§змЙВгаЃК4ЁС10Љ3ЁС4ЃН28ИіЃЌМД28ЃН4ЁС7ЃЛ
Ё
ЭЌРэЕУЃК4ИіСљЮхБпаЮЕФЕуЪ§змЙВгаЃК5ЁС9ЃН45ИіЃЛ
nИіе§СљБпаЮЕФЕуЪ§змЙВгаЃК(n+1)(2n+1)ИіЃЛ
ЙЪД№АИЮЊЃК(n+1)(2n+1)ЃЛ
ЮЪЬтНтОіЃК
ЁпnИіе§Ш§НЧаЮЕФЕуЪ§змЙВгаЃК(n+1)(![]() n+1)ИіЃЛ
n+1)ИіЃЛ
nИіе§ЫФБпаЮЕФЕуЪ§змЙВгаЃК(n+1)(n+1)ИіЃЛ
nИіе§ЮхБпаЮЕФЕуЪ§змЙВгаЃК(n+1)(![]() n+1)ИіЃЛ
n+1)ИіЃЛ
nИіе§СљБпаЮЕФЕуЪ§змЙВгаЃК(n+1)(2n+1)ИіЃЛ
Ё
ЁрnИіе§mБпаЮЕФЕуЪ§змЙВгаЃК![]() ИіЃЛ
ИіЃЛ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЪЕМЪгІгУЃК
гЩЙцТЩЕУЃКnЃН99ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃКmЃН10ЃЎ


 НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЦНааЫФБпаЮABCDжаЃЌABЃН10ЃЌBCЃН16ЃЌcosBЃН![]() ЃЌЕуPЪЧБпBCЩЯЕФЖЏЕуЃЌвдCPЮЊАыОЖЕФдВCгыБпADНЛгкЕуEЁЂFЃЈЕуFдкЕуEЕФгвВрЃЉЃЌЩфЯпCEгыЩфЯпBAНЛгкЕуGЃЎ
ЃЌЕуPЪЧБпBCЩЯЕФЖЏЕуЃЌвдCPЮЊАыОЖЕФдВCгыБпADНЛгкЕуEЁЂFЃЈЕуFдкЕуEЕФгвВрЃЉЃЌЩфЯпCEгыЩфЯпBAНЛгкЕуGЃЎ
ЃЈ1ЃЉЕБдВCОЙ§ЕуAЪБЃЌЧѓCPЕФГЄ
ЃЈ2ЃЉСЊНсAPЃЌЕБAP//CGЪБЃЌЧѓЯвEFЕФГЄ
ЃЈ3ЃЉЕБЁїAGEЪЧЕШбќШ§НЧаЮЪБЃЌЧѓдВCЕФАыОЖГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌtanЁЯBAC![]() tanЁЯABC=1ЃЌЁбOОЙ§AЁЂBСНЕуЃЌЗжБ№НЛACЁЂBCгкDЁЂEСНЕуЃЌШєDE=10ЃЌAB=24ЃЌдђЁбOЕФАыОЖЮЊЃЈ ЃЉ
tanЁЯABC=1ЃЌЁбOОЙ§AЁЂBСНЕуЃЌЗжБ№НЛACЁЂBCгкDЁЂEСНЕуЃЌШєDE=10ЃЌAB=24ЃЌдђЁбOЕФАыОЖЮЊЃЈ ЃЉ
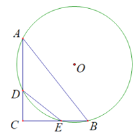
A.![]() B.
B.![]()
C.13D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаОЋзМЗіЦЖЙЄзївбОНјШыЙЅМсНзЖЮЃЌЦЖРЇЕФеХДѓвЏдкФГЕЅЮЛЕФАяЗіЯТЃЌАбвЛЦЌЦТЕиИФдьКѓжжжВСЫДѓгЃЬв.НёФъе§ЪНЩЯЪаЯњЪлЃЌдкЯњЪл30ЬьжаЃЌЕквЛЬьТєГі20ЧЇПЫЃЌЮЊСЫРЉДѓЯњСПЃЌдквЛЖЮЪБМфФкВЩШЁНЕМлДыЪЉЃЌУПЬьБШЧАвЛЬьЖрТєГі4ЧЇПЫЃЎЕБЪлМлВЛБфЪБЃЌЯњЪлСПвВВЛЗЂЩњБфЛЏЃЎвбжЊжжжВЯњЪлДѓгЃЬвЕФГЩБОЮЊ18дЊЃЏЧЇПЫЃЌЩшЕк![]() ЬьЕФЯњЪлМл
ЬьЕФЯњЪлМл![]() дЊЃЏЧЇПЫЃЌ
дЊЃЏЧЇПЫЃЌ![]() гы
гы![]() КЏЪ§ЙиЯЕШчЯТБэЃК
КЏЪ§ЙиЯЕШчЯТБэЃК
БэвЛ
ЬьЪ§ | 1 | 2 | 3 | ЁЁ | ЁЁ | 20 |
ЪлМлЃЈдЊЃЏЧЇПЫЃЉ | 37.5 | 37 | 36.5 | ЁЁ | ЁЁ | 28 |
БэЖў
ЬьЪ§ | 21 | 22 | ЁЁ | ЁЁ | 30 |
ЪлМлЃЈдЊЃЏЧЇПЫЃЉ | 28 | 28 | ЁЁ | ЁЁ | 28 |
ЃЈ1ЃЉЧѓ![]() гы
гы![]() КЏЪ§НтЮіЪНЃЛ
КЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЯњЪлДѓгЃЬвЕкМИЬьЪБЃЌЕБЬьЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉЯњЪлДѓгЃЬвЕФ30ЬьжаЃЌЕБЬьРћШѓВЛЕЭгк
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
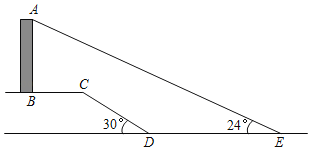
ЁОЬтФПЁПШчЭМЃЌвЊВтСПвЛДЙжБгкЫЎЦНУцЕФНЈжўЮяABЕФИпЖШЃЌаЁУїДгНЈжўЮяЕзЖЫBГіЗЂЃЌбиЫЎЦНЗНЯђЯђгвзп30УзЕНДяЕуCЃЌгжОЙ§вЛЖЮЦТНЧЮЊ30ЁуЃЌГЄЮЊ20УзЕФаБЦТCDЃЌШЛКѓдйбиЫЎЦНЗНЯђЯђгвзпСЫ50УзЕНДяЕуE(AЃЌBЃЌCЃЌDЃЌEОљдкЭЌвЛЦНУцФк)ЃЎдкEДІВтЕУНЈжўЮяЖЅЖЫAЕФбіНЧЮЊ24ЁуЃЌЧѓНЈжўЮяABЕФИпЖШЃЎ(НсЙћБЃСєИљКХЃЌВЮПМЪ§ОнЃКsin24ЁуЁж![]() ЃЌcos24ЁуЁж
ЃЌcos24ЁуЁж![]() ЃЌtan24ЁуЃН
ЃЌtan24ЁуЃН![]() )
)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН3ЃЌBCЃН4ЃЌНЋЖдНЧЯпACШЦЖдНЧЯпНЛЕуOа§зЊЃЌЗжБ№НЛБпADЁЂBCгкЕуEЁЂFЃЌЕуPЪЧБпDCЩЯЕФвЛИіЖЏЕуЃЌЧвБЃГжDPЃНAEЃЌСЌНгPEЁЂPFЃЌЩшAEЃНxЃЈ0ЃМxЃМ3ЃЉЃЎ
ЃЈ1ЃЉЬюПеЃКPCЃНЁЁ ЁЁЃЌFCЃНЁЁ ЁЁЃЛЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЧѓЁїPEFУцЛ§ЕФзюаЁжЕЃЛ
ЃЈ3ЃЉдкдЫЖЏЙ§ГЬжаЃЌPEЁЭPFЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧѓГіxЕФжЕЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
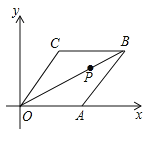
ЁОЬтФПЁПвбжЊСтаЮ![]() дкЦНУцжБНЧзјБъЯЕЕФЮЛжУШчЭМЫљЪОЃЌЖЅЕу
дкЦНУцжБНЧзјБъЯЕЕФЮЛжУШчЭМЫљЪОЃЌЖЅЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌ
жсЕФе§АыжсЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЕу
ЩЯЕФвЛИіЖЏЕуЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌдђ
ЃЌдђ![]() зюаЁжЕЮЊЃЈ ЃЉ
зюаЁжЕЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНУћЭЌбЇЗжБ№Нјаа6ДЮЩфЛїбЕСЗЃЌбЕСЗГЩМЈЃЈЕЅЮЛЃКЛЗЃЉШчЯТБэ
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | ЕкЫФДЮ | ЕкЮхДЮ | ЕкСљНЛ | |
Мз | 9 | 8 | 6 | 7 | 8 | 10 |
вв | 8 | 7 | 9 | 7 | 8 | 8 |
ЖдЫћУЧЕФбЕСЗГЩМЈзїШчЯТЗжЮіЃЌЦфжаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ЫћУЧбЕСЗГЩМЈЕФЦНОљЪ§ЯрЭЌ B. ЫћУЧбЕСЗГЩМЈЕФжаЮЛЪ§ВЛЭЌ
C. ЫћУЧбЕСЗГЩМЈЕФжкЪ§ВЛЭЌ D. ЫћУЧбЕСЗГЩМЈЕФЗНВюВЛЭЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
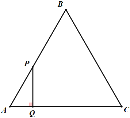
ЁОЬтФПЁПШчЭМЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуPДгЕуAГіЗЂбиAЁњBЁњCТЗОЖдШЫйдЫЖЏЕНЕуCЃЌЕНДяЕуCЪБЭЃжЙдЫЖЏЃЌЙ§ЕуPзїPQЁЭACгкЕуQ. ШєЁїAPQЕФУцЛ§ЮЊyЃЌAQЕФГЄЮЊxЃЌдђЯТСаФмЗДгГyгыxжЎМфЕФДѓжТЭМЯѓЪЧ (ЁЁЁЁ)
A. B.
B.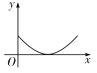 C.
C.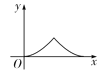 D.
D.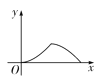
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com