
【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于
【答案】(1)![]() (
(![]() ,x为正整数),
,x为正整数),![]() (
(![]() ,x为正整数);(2)销售大樱桃第18天时,当天的利润最大,最大利润为968元;(3)共有16天的利润不低于950元.
,x为正整数);(2)销售大樱桃第18天时,当天的利润最大,最大利润为968元;(3)共有16天的利润不低于950元.
【解析】
(1)根据表格中的数据,直接写出![]() 与
与![]() 函数解析式,即可;
函数解析式,即可;
(2)分2种情况,①当![]() 时,②当
时,②当![]() 时,分别表示出销售大樱桃当天的利润的函数解析式,即可得到答案;
时,分别表示出销售大樱桃当天的利润的函数解析式,即可得到答案;
(3)分2种情况,①当![]() ,x为正整数时,②当
,x为正整数时,②当![]() ,x为正整数时,分别求出当天利润不低于950元的天数,即可得到答案.
,x为正整数时,分别求出当天利润不低于950元的天数,即可得到答案.
(1)由表1数据可得:![]() (
(![]() ,x为正整数),由表2数据可得:
,x为正整数),由表2数据可得:![]() (
(![]() ,x为正整数);
,x为正整数);
(2)①当![]() 时,
时,
销售大樱桃当天利润为:![]() ,
,
∴![]() 时,当天最大利润为968元,
时,当天最大利润为968元,
②当![]() 时,每天利润都为960元.
时,每天利润都为960元.
答:销售大樱桃第18天时,当天的利润最大,最大利润为968元;
(3)①当![]() ,x为正整数时,令
,x为正整数时,令![]() ,解得:
,解得:![]() =15,
=15,![]() =21(舍),
=21(舍),
∵![]() 的图象开口向下,
的图象开口向下,
∴x=15,16,17,18,19,20时,![]() ,
,
②当![]() ,x为正整数时,
,x为正整数时,![]() ,
,
∴共由16天的利润不低于950元.


科目:初中数学 来源: 题型:
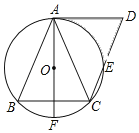
【题目】如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
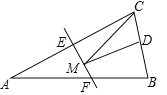
【题目】如图,等腰![]() 的底边
的底边![]() 长为4,面积为12,腰
长为4,面积为12,腰![]() 的垂直平分线
的垂直平分线![]() 分别交边
分别交边![]() 于点
于点![]() ,若点D是的
,若点D是的![]() 中点,点M为线段
中点,点M为线段![]() 上一动点,当
上一动点,当![]() 的周长最小时,
的周长最小时,![]() 长为( )
长为( )
A.1B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
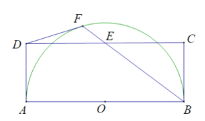
【题目】如图,在矩形ABCD中,边AB是半圆O的直径,点E是CD的中点,BE交半圆O于点F,连接DF.
(1)求证:DF是半圆O的切线;
(2)若AB =8,AD =3,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OAB在平面直角坐标系中的位置如图所示,将△ABO绕原点O逆时针旋转90°得到△OA1B1.
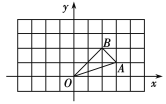
(1)画出△OA1B1,并写出点A1、B1的坐标;
(2)求△ABO绕原点O逆时针旋转90°扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
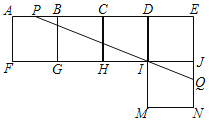
【题目】如图,一“L”型纸片是由5个边长都是10cm的正方形拼接而成,过点I的直线分别与AE,JN交于点P,Q,且“L”型纸片被直线PQ分成面积相等的上下两部分,将该纸片沿BG,CH,DI,IJ折成一个无盖的正方体盒子后,点P,Q之间的距离为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:将正m边形(m≥3)不断向外扩展,每扩展一个正m边形每条边上的点的个数(以下简称“点数”)就增加一个,则n个正m边形的点数总共有多少个?
问题探究:为了解决上面的问题,我们将采取将一般问题特殊化的策略,先从简单和具体的情形入手:
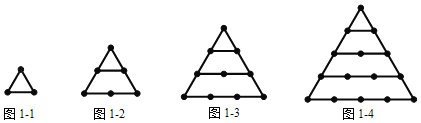
探究一:n个正三角形的点数总共有多少个?
如图1﹣1,1个正三角形的点数总共有3个;如图1﹣2,2个正三角形的点数总共有6个;如图1﹣3,3个正三角形的点数总共有10个;…;n个正三角形的点数总共有 个.
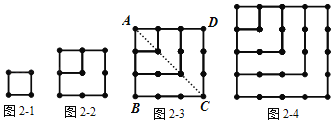
探究二:n个正四边形的点数总共有多少个?
如图2﹣1,1个正四边形的点数总共有4个;如图2﹣2,2个正四边形的点数总共有9个;
如图2﹣3,连接AC,得到两个三角形△ABC和△ADC,这两个三角形相同之处在于,BC边与CD边都有相同个数的点,即4个点,并且与BC、CD平行的边上依次减少一个点直至顶点A,每个三角形都有10个点,两个三角形就是2×10个点.因为这两个三角形在AC上有4个点重合,所以3个正四边形的点数总共有2×10﹣4=16(个).
如图2﹣4,4个正四边形的点数总共有 个;……n个正四边形的点数总共有 个.
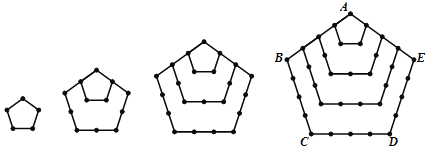
探究三:n个正五边形的点数总共有多少个?
类比探究二的方法,求4个正五边形的点数总共有多少个?并叙述你的探究过程.
n个正五边形的点数总共有 个.
探究四:n个正六边形的点数总共有 个.
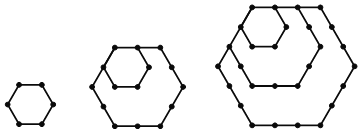
问题解决:n个正m边形的点数总共有 个.
实际应用:若99个正m边形的点数总共有39700个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(新洲区月考)如图1,AB为半圆O的直径,C为圆弧上一点,过点C的直线与AB的延长线交于点E,AD⊥CE于点D,AC平分∠DAB.
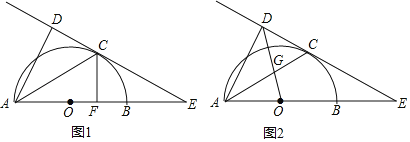
(1)求证:CE是⊙O的切线.
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
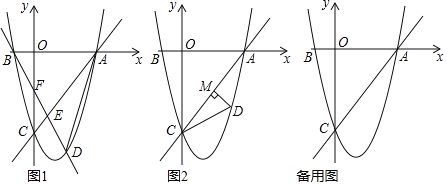
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣4与抛物线y=
x﹣4与抛物线y=![]() +bx+c交于坐标轴上两点A、C,抛物线与x轴另一交点为点B;
+bx+c交于坐标轴上两点A、C,抛物线与x轴另一交点为点B;
(1)求抛物线解析式;
(2)若动点D在直线AC下方的抛物线上;
①作直线BD,交线段AC于点E,交y轴于点F,连接AD;求△ADE与△CEF面积差的最大值,及此时点D的坐标;
②如图2,作DM⊥直线AC,垂足为点M,是否存在点D,使△CDM中某个角恰好是∠ACO的一半?若存在,直接写出点D的横坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com