
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽÖąÏßyĢ―![]() xĐ4ÓëÅŨÎïÏßyĢ―
xĐ4ÓëÅŨÎïÏßyĢ―![]() +bx+c―ŧÓÚŨøąęÖáÉÏÁ―ĩãAĄĒCĢŽÅŨÎïÏßÓëxÖáÁíŌŧ―ŧĩãΊĩãBĢŧ
+bx+c―ŧÓÚŨøąęÖáÉÏÁ―ĩãAĄĒCĢŽÅŨÎïÏßÓëxÖáÁíŌŧ―ŧĩãΊĩãBĢŧ
ĢĻ1ĢĐĮóÅŨÎïÏß―âÎöĘ―Ģŧ
ĢĻ2ĢĐČôķŊĩãDÔÚÖąÏßACÏ·―ĩÄÅŨÎïÏßÉÏĢŧ
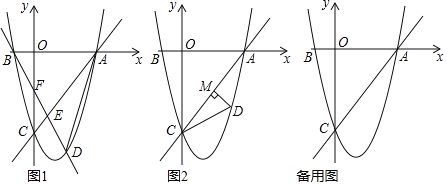
ĒŲŨũÖąÏßBDĢŽ―ŧÏßķÎACÓÚĩãEĢŽ―ŧyÖáÓÚĩãFĢŽÁŽ―ÓADĢŧĮóĄũADEÓëĄũCEFÃæŧýēîĩÄŨîīóÖĩĢŽž°īËĘąĩãDĩÄŨøąęĢŧ
ĒÚČįÍž2ĢŽŨũDMĄÍÖąÏßACĢŽīđŨãΊĩãMĢŽĘĮ·ņīæÔÚĩãDĢŽĘđĄũCDMÖÐÄģļö―ĮĮĄšÃĘĮĄÏACOĩÄŌŧ°ëĢŋČôīæÔÚĢŽÖą―ÓÐīģöĩãDĩÄšáŨøąęĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐyĢ―![]() Ģŧ
Ģŧ
ĢĻ2ĢĐĒŲĩąmĢ―![]() ĘąĢŽSĄũADEĐSĄũCEFĩÄŨîīóÖĩΊ
ĘąĢŽSĄũADEĐSĄũCEFĩÄŨîīóÖĩΊ![]() ĢŽīËĘąĩãDŨøąęΊĢĻ
ĢŽīËĘąĩãDŨøąęΊĢĻ![]() ĢŽ
ĢŽ![]() ĢĐĢŧ
ĢĐĢŧ
ĒÚīæÔÚĢŽĩãDĩÄšáŨøąęΊĩãDšáŨøąęΊ![]() ŧō
ŧō![]() ĢŪ
ĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐÏČĮóģöCĢĻ0ĢŽĐ4ĢĐAĢĻ3ĢŽ0ĢĐĢŽČŧšóīúČëyĢ―![]() +bx+cĢŽīÓķøĮóģöÅŨÎïÏß―âÎöĘ―Ģŧ
+bx+cĢŽīÓķøĮóģöÅŨÎïÏß―âÎöĘ―Ģŧ
ĢĻ2ĢĐĒŲÉčDĢĻmĢŽ![]() ĢĐĢŽÔōtanĄÏABDĢ―
ĢĐĢŽÔōtanĄÏABDĢ―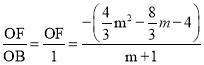 ĢŽČŧšóÓÃmĩÄīúĘýĘ―ąíĘūĄũADEÓëĄũCEFÃæŧýēîĢŽĀûÓÃķþīΚŊĘýŨîÖĩĮóģöŨîīóÖĩĢŧ
ĢŽČŧšóÓÃmĩÄīúĘýĘ―ąíĘūĄũADEÓëĄũCEFÃæŧýēîĢŽĀûÓÃķþīΚŊĘýŨîÖĩĮóģöŨîīóÖĩĢŧ
ĒÚŨũĄÏACOĩÄÆ―·ÖÏßCP―ŧxÖáÓÚĩãPĢŽđýPŨũPHĄÍACÓÚĩãHĢŪĮóģötanĄÏPCHĢ―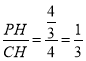 ĢŽČŧšó·ÖÁ―ÖÖĮéŋöĖÖÂÛĢšĒņĢŪĩąĄÏMCDĢ―
ĢŽČŧšó·ÖÁ―ÖÖĮéŋöĖÖÂÛĢšĒņĢŪĩąĄÏMCDĢ―![]() ĄÏACOĢ―ĄÏPCHĘąĢŽĒōĢŪĩąĄÏMDCĢ―
ĄÏACOĢ―ĄÏPCHĘąĢŽĒōĢŪĩąĄÏMDCĢ―![]() ĄÏACOĢ―ĄÏPCHĘąĢŪ
ĄÏACOĢ―ĄÏPCHĘąĢŪ
ĢĻ1ĢĐķÔÓÚyĢ―![]() xĐ4ĢŽÁîxĢ―0ĢŽÔōyĢ―Đ4ËųŌÔCĢĻ0ĢŽĐ4ĢĐĢŧ
xĐ4ĢŽÁîxĢ―0ĢŽÔōyĢ―Đ4ËųŌÔCĢĻ0ĢŽĐ4ĢĐĢŧ
ÁîyĢ―0ĢŽÔōxĢ―3ĢŽ
ĄāAĢĻ3ĢŽ0ĢĐĢŧ
°ŅĩãAĄĒCŨøąęīúČëÅŨÎïÏß―âÎöĘ―ĢŽ
ĩÃĢš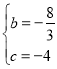 ―âĩÃ
―âĩÃ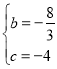 ĢŽ
ĢŽ
ĄāÅŨÎïÏß―âÎöĘ―ÎŠyĢ―![]() Ģŧ
Ģŧ
ĢĻ2ĢĐÉčDĢĻmĢŽ![]() ĢĐĢŽ0ĢžmĢž3
ĢĐĢŽ0ĢžmĢž3
ĒŲÁŽ―ÓODĢŽŌōΊBĢĻĐ1ĢŽ0ĢĐĢŽDĢĻmĢŽ![]() ĢĐ
ĢĐ
tanĄÏABDĢ―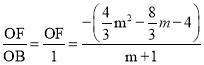 ĢŽ
ĢŽ
ĄāOFĢ―Đ![]() ĢĻmĐ3ĢĐĢŽ
ĢĻmĐ3ĢĐĢŽ
ÓÖOAĢ―3ĢŽOCĢ―4ĢŽ
ĄāSĄũADEĐSĄũCEFĢ―SËÄąßÐÎAOFDĐSĄũAOCĢ―![]() AO|yD|+
AO|yD|+![]() OF|xD|Đ
OF|xD|Đ![]() OAOC
OAOC
Ģ―![]() [3ĢĻĐ
[3ĢĻĐ![]() m2+
m2+![]() m+4ĢĐĐ
m+4ĢĐĐ![]() ĢĻmĐ3ĢĐmĐ3ĄÁ4]
ĢĻmĐ3ĢĐmĐ3ĄÁ4]
Ģ―Đ![]() m2+6m
m2+6m
Ģ―Đ![]() ĢĻmĐ
ĢĻmĐ![]() ĢĐ2+
ĢĐ2+![]() ĢŽ
ĢŽ
ËųŌÔĩąmĢ―![]() ĘąĢŽSĄũADEĐSĄũCEFĩÄŨîīóÖĩΊ
ĘąĢŽSĄũADEĐSĄũCEFĩÄŨîīóÖĩΊ![]() ĢŽīËĘąĩãDŨøąęΊ
ĢŽīËĘąĩãDŨøąęΊ![]() Ģŧ
Ģŧ
ĒÚīæÔÚĢŽĩãDĩÄšáŨøąęΊĩãDšáŨøąęΊ![]() ŧō
ŧō![]() ĢŪ
ĢŪ
ŨũĄÏACOĩÄÆ―·ÖÏßCP―ŧxÖáÓÚĩãPĢŽđýPŨũPHĄÍACÓÚĩãHĢŪ
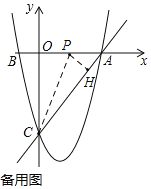
ÔōCHĢ―COĢ―4ĢŽOPĢ―PHĢŽ
ÉčOPĢ―PHĢ―xĢŽÔōPAĢ―3ĐxĢŽ
ĄßOCĢ―4ĢŽOAĢ―3ĢŽ
ĄāACĢ―5ĢŽAHĢ―1ĢŽ
ÔÚRtĄũPHAÖÐĢŽ
PH2+AH2Ģ―AP2ĢŽ
žī/span>x2+12Ģ―ĢĻ3ĐxĢĐ2ĢŽ
―âĩÃxĢ―![]() ĢŽ
ĢŽ
ĄātanĄÏPCHĢ―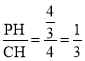 ĢŽ
ĢŽ
đýĩãDŨũDGĄÍxÖáÓÚĩãGĢŽđýĩãMŨũMEĄÎxÖáĢŽÓëyÖá―ŧÓÚĩãEĢŽÓëDG―ŧÓÚĩãFĢŪ
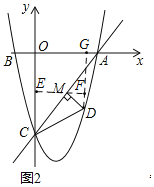
ÉčMĢĻmĢŽ![]() ĢĐĢŽÔōMEĢ―mĢŽFGĢ―OEĢ―
ĢĐĢŽÔōMEĢ―mĢŽFGĢ―OEĢ―![]() ĢŽCEĢ―
ĢŽCEĢ―![]() ĢŽ
ĢŽ
ĄßDMĄÍÖąÏßACĢŽ
ĄāĄũCEMĄŨĄũMFDĢŽ
Ąā![]() ĢŽ
ĢŽ
ĒņĢŪĩąĄÏMCDĢ―![]() ĄÏACOĢ―ĄÏPCHĘąĢŽ
ĄÏACOĢ―ĄÏPCHĘąĢŽ
tanĄÏMCDĢ―tanĄÏPCHĢ―![]() ĢŽ
ĢŽ
Ąā![]() ĢŽžī
ĢŽžī![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄāMFĢ―![]() CEĢ―
CEĢ―![]() ĢŽDFĢ―
ĢŽDFĢ―![]() MEĢ―
MEĢ―![]() ĢŽ
ĢŽ
ĄāEFĢ―EM+MFĢ―m+![]() Ģ―
Ģ―![]() ĢŽDGĢ―DF+FGĢ―
ĢŽDGĢ―DF+FGĢ―![]() m+ĢĻ
m+ĢĻ![]() ĢĐĢ―Đm+4ĢŽ
ĢĐĢ―Đm+4ĢŽ
ĄāDĢĻ![]() ĢŽmĐ4ĢĐĢŽ
ĢŽmĐ4ĢĐĢŽ
―ŦĩãDŨøąęīúČëyĢ―![]() ĢŽ
ĢŽ
mĐ4Ģ―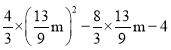 ĢŽ
ĢŽ
―âĩÃmĢ―0ĢĻÉáČĨĢĐŧōmĢ―![]()
ĒōĢŪĩąĄÏMDCĢ―![]() ĄÏACOĢ―ĄÏPCHĘąĢŽ
ĄÏACOĢ―ĄÏPCHĘąĢŽ
tanĄÏMDCĢ―tanĄÏPCHĢ―![]() ĢŽ
ĢŽ
žī![]() ĢŽ
ĢŽ
Ąā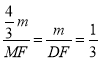 ĢŽ
ĢŽ
MFĢ―4mĢŽDFĢ―3mĢŽ
ĄāEFĢ―EM+MFĢ―m+4mĢ―5mĢŽ
DGĢ―DF+FGĢ―3mĐ![]() ĢŽ
ĢŽ
ĄāDĢĻ5mĢŽ ![]() ĢĐĢŽ
ĢĐĢŽ
―ŦĩãDŨøąęīúČëyĢ―![]() ĢŽ
ĢŽ
![]() ĢŽ
ĢŽ
―âĩÃxĢ―0ĢĻÉáČĨĢĐŧōxĢ―![]() Ģŧ
Ģŧ
ŨÛÉÏĢŽĩãDšáŨøąęΊ![]() ŧō
ŧō![]() ĢŪ
ĢŪ



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÄģĘÐūŦŨž·öÆķđĪŨũŌŅū―øČëđĨžá―ŨķÎĢŽÆķĀ§ĩÄÕÅīóŌŊÔÚÄģĩĨÎŧĩÄ°ï·öÏÂĢŽ°ŅŌŧÆŽÆÂĩØļÄÔėšóÖÖÖēÁËīóÓĢĖŌ.―ņÄęÕýĘ―ÉÏĘÐÏúĘÛĢŽÔÚÏúĘÛ30ĖėÖÐĢŽĩÚŌŧĖėÂôģö20Į§ŋËĢŽÎŠÁËĀĐīóÏúÁŋĢŽÔÚŌŧķÎĘąžäÄÚēÉČĄ―ĩžÛīëĘĐĢŽÃŋĖėąČĮ°ŌŧĖėķāÂôģö4Į§ŋËĢŪĩąĘÛžÛēŧąäĘąĢŽÏúĘÛÁŋŌēēŧ·ĒÉúąäŧŊĢŪŌŅÖŠÖÖÖēÏúĘÛīóÓĢĖŌĩÄģÉąūΊ18ÔŠĢŊĮ§ŋËĢŽÉčĩÚ![]() ĖėĩÄÏúĘÛžÛ
ĖėĩÄÏúĘÛžÛ![]() ÔŠĢŊĮ§ŋËĢŽ
ÔŠĢŊĮ§ŋËĢŽ![]() Óë
Óë![]() šŊĘýđØÏĩČįÏÂąíĢš
šŊĘýđØÏĩČįÏÂąíĢš
ąíŌŧ
ĖėĘý | 1 | 2 | 3 | ĄĄ | ĄĄ | 20 |
ĘÛžÛĢĻÔŠĢŊĮ§ŋËĢĐ | 37.5 | 37 | 36.5 | ĄĄ | ĄĄ | 28 |
ąíķþ
ĖėĘý | 21 | 22 | ĄĄ | ĄĄ | 30 |
ĘÛžÛĢĻÔŠĢŊĮ§ŋËĢĐ | 28 | 28 | ĄĄ | ĄĄ | 28 |
ĢĻ1ĢĐĮó![]() Óë
Óë![]() šŊĘý―âÎöĘ―Ģŧ
šŊĘý―âÎöĘ―Ģŧ
ĢĻ2ĢĐĮóÏúĘÛīóÓĢĖŌĩÚžļĖėĘąĢŽĩąĖėĩÄĀûČóŨîīóĢŋŨîīóĀûČóĘĮķāÉŲĢŋ
ĢĻ3ĢĐÏúĘÛīóÓĢĖŌĩÄ30ĖėÖÐĢŽĩąĖėĀûČóēŧĩÍÓÚ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋžŨĄĒŌŌÁ―ÃûÍŽŅ§·Öąð―øÐÐ6īÎÉäŧũŅĩÁ·ĢŽŅĩÁ·ģÉžĻĢĻĩĨÎŧĢšŧ·ĢĐČįÏÂąí
ĩÚŌŧīÎ | ĩÚķþīÎ | ĩÚČýīÎ | ĩÚËÄīÎ | ĩÚÎåīÎ | ĩÚÁų―ŧ | |
žŨ | 9 | 8 | 6 | 7 | 8 | 10 |
ŌŌ | 8 | 7 | 9 | 7 | 8 | 8 |
ķÔËûÃĮĩÄŅĩÁ·ģÉžĻŨũČįÏ·ÖÎöĢŽÆäÖÐËĩ·ĻÕýČ·ĩÄĘĮĢĻĄĄĄĄĢĐ
A. ËûÃĮŅĩÁ·ģÉžĻĩÄÆ―ūųĘýÏāÍŽ B. ËûÃĮŅĩÁ·ģÉžĻĩÄÖÐÎŧĘýēŧÍŽ
C. ËûÃĮŅĩÁ·ģÉžĻĩÄÖÚĘýēŧÍŽ D. ËûÃĮŅĩÁ·ģÉžĻĩÄ·―ēîēŧÍŽ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽ![]() ĘĮ
ĘĮ![]() ĩÄÖąūķĢŽ
ĩÄÖąūķĢŽ![]() ĘĮÉÏ°ëÔēĩÄÏŌĢŽđýĩã
ĘĮÉÏ°ëÔēĩÄÏŌĢŽđýĩã![]() Ũũ
Ũũ![]() ĩÄĮÐÏß
ĩÄĮÐÏß![]() ―ŧ
―ŧ![]() ĩÄŅÓģĪÏßÓÚĩã
ĩÄŅÓģĪÏßÓÚĩã![]() ĢŽđýĩã
ĢŽđýĩã![]() ŨũĮÐÏß
ŨũĮÐÏß![]() ĩÄīđÏßĢŽīđŨãΊ
ĩÄīđÏßĢŽīđŨãΊ![]() ĢŽĮŌÓë
ĢŽĮŌÓë![]() ―ŧÓÚĩã
―ŧÓÚĩã![]() ĢŽÉč
ĢŽÉč![]() ĢŽ
ĢŽ![]() ĩÄķČĘý·ÖąðĘĮ
ĩÄķČĘý·ÖąðĘĮ![]() .
.
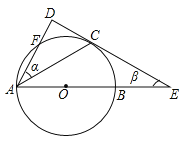
![]() ÓÚŽ
ÓÚŽ![]() ĩÄīúĘýĘ―ąíĘū
ĩÄīúĘýĘ―ąíĘū![]() ĢŽēĒÖą―ÓÐīģö
ĢŽēĒÖą―ÓÐīģö![]() ĩÄČĄÖĩ·ķΧĢŧ
ĩÄČĄÖĩ·ķΧĢŧ
![]() ÁŽ―Ó
ÁŽ―Ó![]() Óë
Óë![]() ―ŧÓÚĩã
―ŧÓÚĩã![]() ĢŽĩąĩã
ĢŽĩąĩã![]() ĘĮ
ĘĮ![]() ĩÄÖÐĩãĘąĢŽĮó
ĩÄÖÐĩãĘąĢŽĮó![]() ĩÄÖĩ.
ĩÄÖĩ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽAĢĻ4ĢŽ3ĢĐĘĮ·īąČĀýšŊĘýy=![]() ÔÚĩÚŌŧÏóÏÞÍžÏóÉÏŌŧĩãĢŽÁŽ―ÓOAĢŽđýAŨũABĄÎxÖáĢŽ―ØČĄAB=OAĢĻBÔÚAÓŌēāĢĐĢŽÁŽ―ÓOBĢŽ―ŧ·īąČĀýšŊĘýy=
ÔÚĩÚŌŧÏóÏÞÍžÏóÉÏŌŧĩãĢŽÁŽ―ÓOAĢŽđýAŨũABĄÎxÖáĢŽ―ØČĄAB=OAĢĻBÔÚAÓŌēāĢĐĢŽÁŽ―ÓOBĢŽ―ŧ·īąČĀýšŊĘýy=![]() ĩÄÍžÏóÓÚĩãPĢŪ
ĩÄÍžÏóÓÚĩãPĢŪ
ĢĻ1ĢĐĮó·īąČĀýšŊĘýy=![]() ĩÄąíīïĘ―Ģŧ
ĩÄąíīïĘ―Ģŧ
ĢĻ2ĢĐĮóĩãBĩÄŨøąęĢŧ
ĢĻ3ĢĐĮóĄũOAPĩÄÃæŧýĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
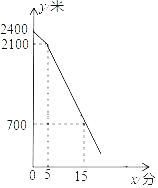
ĄūĖâÄŋĄŋšŪžŲÖÐĢŽÐĄÍõÏōÐĄĀî―čŌŧąūĘýŅ§ÅāÓÅŨĘÁÏĢŽĩŦÏāŧĨÕŌēŧĩ―ķÔ·―ĩÄžŌĢŽĩįŧ°ÖÐÁ―ČËÉĖÁŋĢŽŨßÁ―žŌÖŪžäģĪķČΊ2400ÃŨĩÄŌŧĖõ·ĢŽÏāÏōķøÐÐĢŪÐĄĀîÔÚÐĄÍõģö·Ē5·ÖÖÓšóīøÉÏĘýŅ§ÅāÓÅŨĘÁÏģö·ĒĢŪÔÚÕûļöÐÐŨßđýģĖÖÐĢŽÁ―ČËūųąĢģÖļũŨÔĩÄËŲķČÔČËŲÐÐŨßĢŪÁ―ČËÏāūāĩÄ·ģĖyĢĻĩĨÎŧĢšÃŨĢĐÓëÐĄÍõģö·ĒĩÄĘąžäxĢĻĩĨÎŧĢš·ÖĢĐÖŪžäĩÄđØÏĩČįÍžËųĘūĢŽÔōÁ―ČËÏāÓöĘąĢŽÐĄĀîŨßÁË_____ÃŨĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCΊĩČąßČý―ĮÐÎĢŽĩãPīÓĩãAģö·ĒŅØAĄúBĄúC·ūķÔČËŲÔËķŊĩ―ĩãCĢŽĩ―īïĩãCĘąÍĢÖđÔËķŊĢŽđýĩãPŨũPQĄÍACÓÚĩãQ. ČôĄũAPQĩÄÃæŧýΊyĢŽAQĩÄģĪΊxĢŽÔōÏÂÁÐÄÜ·īÓģyÓëxÖŪžäĩÄīóÖÂÍžÏóĘĮ (ĄĄĄĄ)
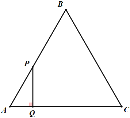
A. B.
B.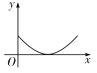 C.
C.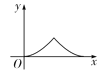 D.
D.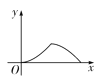
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĄ°đđÔėÍžÐÎ―âĖ⥹ĢŽËüĩÄÓĶÓÃĘŪ·Öđã·šĢŽĖØąðĘĮÓÐÐĐžžĮÉÐÔšÜĮŋĩÄĖâÄŋĢŽČįđûēŧÄÜ·ĒÏÖĖâÄŋÖÐËųŌþšŽĩÄžļšÎŌâŌåĢŽķøÓÃÍĻģĢĩÄīúĘý·―·ĻČĨËžŋžĢŽūģĢČÃÎŌÃĮĘÖŨãÎÞīëĢŽÄŅŌÔÏÂĘÖĢŽÕâĘąĢŽČįđûÄÜŨŠŧŧ˞ΎĢŽ·ĒÏÖĖâÄŋÖÐŌþšŽĩÄžļšÎĖõžþĢŽÍĻđýđđÔėĘĘšÏĩÄžļšÎÍžÐÎĢŽ―ŦŧáĩÃĩ―Ę°ëđĶąķĩÄЧđûĢŽÏÂÃæ―éÉÜÁ―ÔōĘĩĀýĢš
ĘĩĀýŌŧĢš1876ÄęĢŽÃĀđúŨÜÍģŲĪ·ĮķûĩÂĀûÓÃĘĩĀýŌŧÍžÖĪÃũÁËđīđÉķĻĀíĢšÓÉ![]() ËÄąßÐÎ
ËÄąßÐÎ![]() ĩÃ
ĩÃ![]() ĢŽŧŊžōĩÃĢš
ĢŽŧŊžōĩÃĢš![]() ĢŪ
ĢŪ
ĘĩĀýķþĢšÅ·žļĀïĩÃĩÄĄķžļšÎÔąūĄ·žĮÔØĢŽđØÓÚ![]() ĩÄ·―ģĖ
ĩÄ·―ģĖ![]() ĩÄÍž―â·ĻĘĮĢšŧ
ĩÄÍž―â·ĻĘĮĢšŧ![]() ĢŽĘđ
ĢŽĘđ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÔŲÔÚÐąąß
ĢŽÔŲÔÚÐąąß![]() ÉÏ―ØČĄ
ÉÏ―ØČĄ![]() ĢŽÔō
ĢŽÔō![]() ĩÄģĪūÍĘĮļ÷―ģĖĩÄŌŧļöÕýļų(ČįĘĩĀýķþÍž)ĢŪ
ĩÄģĪūÍĘĮļ÷―ģĖĩÄŌŧļöÕýļų(ČįĘĩĀýķþÍž)ĢŪ
ļųūÝŌÔÉÏÔÄķÁēÄÁÏŧØīðÏÂÃæĩÄÎĘĖâĢš
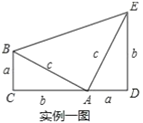
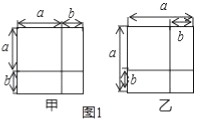
ĢĻ1ĢĐČįÍž1ĢŽĮëĀûÓÃÍžÐÎÖÐÃæŧýĩÄĩČÁŋđØÏĩĢŽÐīģöžŨÍžŌŠÖĪÃũĩÄĘýŅ§đŦĘ―ĘĮĄĄĄĄĄĄĄĄĢŽŌŌÍžŌŠÖĪÃũĩÄĘýŅ§đŦĘ―ĘĮĄĄĄĄĄĄĄĄĢŽĖåÏÖĩÄĘýŅ§ËžÏëĘĮĄĄĄĄĄĄĄĄĢŧ
ĢĻ2ĢĐČįÍž2ĢŽ°īÕÕĘĩĀýķþĩÄ·―Ę―đđÔė![]() ĢŽÁŽ―Ó
ĢŽÁŽ―Ó![]() ĢŽĮëÓÚŽŨÖÄļ
ĢŽĮëÓÚŽŨÖÄļ![]() ĄĒ
ĄĒ![]() ĩÄīúĘýĘ―ąíĘū
ĩÄīúĘýĘ―ąíĘū![]() ĩÄģĪĢŽ
ĩÄģĪĢŽ![]() ĩÄąíīïĘ―ÄÜšÍŌŅŅ§ĩÄĘēÃīÖŠĘķÏāÁŠÏĩĢŧ
ĩÄąíīïĘ―ÄÜšÍŌŅŅ§ĩÄĘēÃīÖŠĘķÏāÁŠÏĩĢŧ
ĢĻ3ĢĐČįÍž3ĢŽŌŅÖŠ![]() ĢŽ
ĢŽ![]() ΊֹūķĢŽĩã
ΊֹūķĢŽĩã![]() ΊÔēÉÏŌŧĩãĢŽđýĩã
ΊÔēÉÏŌŧĩãĢŽđýĩã![]() Ũũ
Ũũ![]() ÓÚĩã
ÓÚĩã![]() ĢŽÁŽ―Ó
ĢŽÁŽ―Ó![]() ĢŽÉč
ĢŽÉč![]() ĢŽ
ĢŽ![]() ĢŽĮóÖĪĢš
ĢŽĮóÖĪĢš![]() ĢŪ
ĢŪ
 ĄĄĄĄĄĄĄĄ
ĄĄĄĄĄĄĄĄ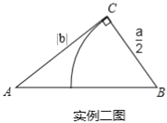
 ĄĄĄĄĄĄĄĄ
ĄĄĄĄĄĄĄĄ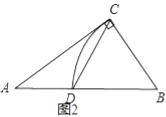 ĄĄĄĄĄĄĄĄ
ĄĄĄĄĄĄĄĄ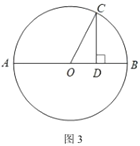
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÕý·―ÐÎÍøļņÖÐĩÄÃŋļöÐĄÕý·―ÐÎĩÄąßģĪķžĘĮ1ĢŽÃŋļöÐĄÕý·―ÐÎĩÄķĨĩã―ÐŨöļņĩãĢŪĄũABCĩÄČýļöķĨĩãAĢŽBĢŽCķžÔÚļņĩãÉÏĢŪ―ŦĄũABCČÆĩãA°īËģĘąÕë·―ÏōÐýŨŠ90ĄãĩÃĩ―ĄũABĄäCĄäĢŪ

ĢĻ1ĢĐÔÚÕý·―ÐÎÍøļņÖÐĢŽŧģöĄũABĄäCĄäĢŧ
ĢĻ2ĢĐžÆËãÏßķÎABÔÚąäŧŧĩ―ABĄäĩÄđýģĖÖÐÉĻđýĩÄĮøÓōĩÄÃæŧýĢŪ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com