
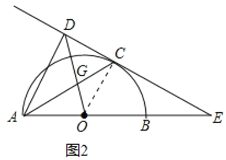
【题目】(新洲区月考)如图1,AB为半圆O的直径,C为圆弧上一点,过点C的直线与AB的延长线交于点E,AD⊥CE于点D,AC平分∠DAB.
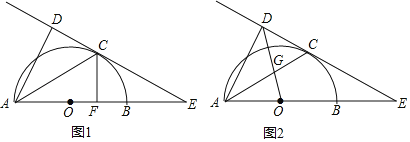
(1)求证:CE是⊙O的切线.
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
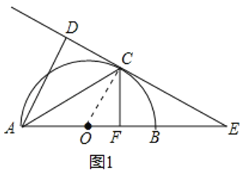
(3)如图2,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接OC,由AC为角平分线得到一对角相等,再由等边对等角得到一对角相等,等量代换得到一对内错角相等,进而得到OC与AD平行,由AD与CE垂直,得到OC与CE垂直,即可得证;
(2)由OB=BE,根据半径OA的长求出OE的长,在直角三角形OCE中,根据OC![]() OE得到∠E=30°,在直角三角形CEF中,利用30°所对的直角边等于斜边的一半即可求出CF的长;
OE得到∠E=30°,在直角三角形CEF中,利用30°所对的直角边等于斜边的一半即可求出CF的长;
(3)连接OC,由(1)得到OC与AD平行,进而得到三角形OCG与三角形ADG相似,三角形OCE与三角形ADE相似,由相似得比例求出![]() 的值,即可确定出sinE的值.
的值,即可确定出sinE的值.
(1)连接OC,
∵AC平分∠DAB,
∴∠DAC=∠CAO,
∵OA=OC,
∴∠OAC=∠ACO,
∵∠DAC=∠ACO,
∴OC∥AD,
∵AD⊥CE,
∴OC⊥CE,
∴CE为⊙O的切线;
(2)∵AB=6,OB=BE,
∴OE=6,
在Rt△OCE中,
∵OC=3,OE=6,
∴∠E=30°,
∴CE=3![]() ,
,
∴在Rt△CFE中,CF![]() ;
;
(3)连接OC,
由(1)得OC∥AD,
∴△COG∽△ADG,△COE∽△DAE,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵AO=CO,
∴![]() ,
,
在Rt△OCE中,sinE![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
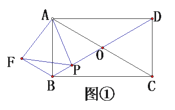
如图①,矩形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,且
,且![]() ,点
,点![]() 为线段
为线段![]() 上任意一点,以
上任意一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() ,则
,则![]() 与
与![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)类比延伸
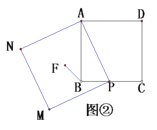
如图②,在正方形![]() 中,点
中,点![]() 为
为![]() 边上任意一点,以
边上任意一点,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 为正方形
为正方形![]() 的中心,连接
的中心,连接![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(3)拓展迁移
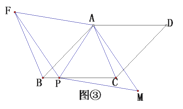
如图③,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,以
边上一点,以![]() 为对角线作菱形
为对角线作菱形![]() ,满足
,满足![]() ,连接
,连接![]() ,猜想
,猜想![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
查看答案和解析>>
科目:初中数学 来源: 题型:
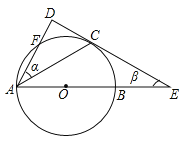
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
![]() 连接
连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由![]() 四边形
四边形![]() 得
得![]() ,化简得:
,化简得:![]() .
.
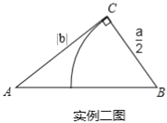
实例二:欧几里得的《几何原本》记载,关于![]() 的方程
的方程![]() 的图解法是:画
的图解法是:画![]() ,使
,使![]() ,
,![]() ,
,![]() ,再在斜边
,再在斜边![]() 上截取
上截取![]() ,则
,则![]() 的长就是该方程的一个正根(如实例二图).
的长就是该方程的一个正根(如实例二图).
根据以上阅读材料回答下面的问题:
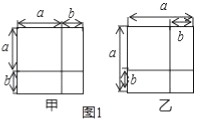
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是 ,体现的数学思想是 ;
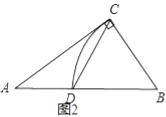
(2)如图2,按照实例二的方式构造![]() ,连接
,连接![]() ,请用含字母
,请用含字母![]() 、
、![]() 的代数式表示
的代数式表示![]() 的长,
的长,![]() 的表达式能和已学的什么知识相联系;
的表达式能和已学的什么知识相联系;
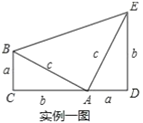
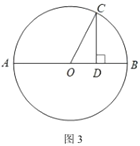
(3)如图3,已知![]() ,
,![]() 为直径,点
为直径,点![]() 为圆上一点,过点
为圆上一点,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com