
【题目】任何大于1的正整数m的三次幂均可分裂成m个连续奇数的和。如:23=3+5、33=7+9+11、43=13+15+17+19……依此规律,若m3分裂后其中有一个奇数是2019,则m的值是_____.
科目:初中数学 来源: 题型:
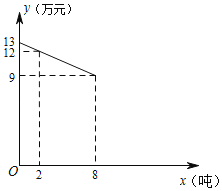
【题目】温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅,包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(2≤x≤10,单位:吨)之间的函数关系如图所示.
(1)若杨梅的销售量为6吨时,它的平均销售价格是每吨多少万元?
(2)当销售数量为多少时,该经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)
(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是y=![]() x+3(2≤x≤10).
x+3(2≤x≤10).
①当该公司买入杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?
②该公司买入杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示:
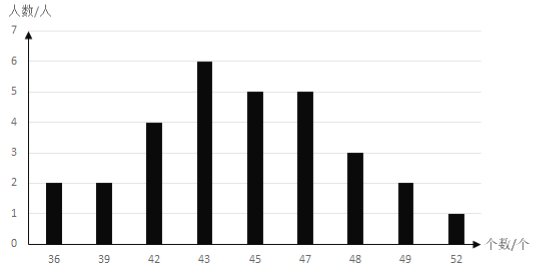
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
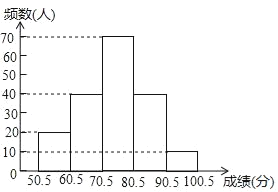
【题目】为在中小学生中普及交通法规常识,倡导安全出行,某市教育局在全市范围内组织七年级学生进行了一次“交规记心间”知识竞赛.为了解市七年级学生的竟赛成绩,随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和如图所示的频数分布直方图(频数分布直方图中有一处错误).
组别(单位:分) | 频数 | 频率 |
50.5~60.5 | 20 | 0.1 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 70 | b |
80.5~90.5 | a | 0.3 |
90.5~100.5 | 10 | 0.05 |
请根据图表信息回答下列问题:
(1)在频数分布表中,a= ,b= .
(2)指出频数分布直方图中的错误,并在图上改正;
(3)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问:甲同学的成绩应在什么范围?
(4)全市共有5000名七年级学生,若规定成绩在80分以上(不含80分)为优秀,估计这次竞赛中成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
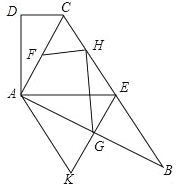
(1)求证:AC2=CD·BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
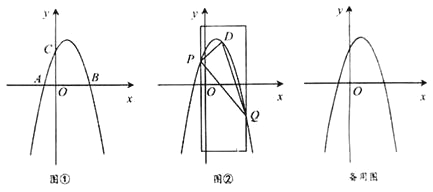
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
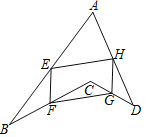
【题目】如图,在“飞镖形”ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)“飞镖形”ABCD满足条件 时,四边形EFGH是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com