
【题目】(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
【答案】解:(1)∵点E是AB的中点,OA=2,AB=4,∴点E的坐标为(2,2)。
将点E的坐标代入![]() ,可得k=4。
,可得k=4。
∴反比例函数解析式为:![]() 。
。
∵点F的横坐标为4,∴点F的纵坐标![]() 。
。
∴点F的坐标为(4,1)。
(2)结合图形可设点E坐标为(![]() ,2),点F坐标为(4,
,2),点F坐标为(4,![]() ),
),
则CF=![]() ,BF=DF=2﹣
,BF=DF=2﹣![]() ,ED=BE=AB﹣AE=4﹣
,ED=BE=AB﹣AE=4﹣![]() ,
,
在Rt△CDF中,![]() 。
。
由折叠的性质可得:BE=DE,BF=DF,∠B=∠EDF=90°,
∵∠CDF+∠EDG=90°,∠GED+∠EDG=90°,∴∠CDF=∠GED。
又∵∠EGD=∠DCF=90°,∴△EGD∽△DCF。
∴![]() ,即
,即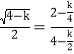 。
。
∴![]() =1,解得:k=3。
=1,解得:k=3。
【解析】
(1)根据点E是AB中点,可求出点E的坐标,将点A的坐标代入反比例函数解析式可求出k的值,再由点F的横坐标为4,可求出点F的纵坐标,继而得出答案。
(2)证明∠GED=∠CDF,然后利用两角法可判断△EGD∽△DCF,设点E坐标为(![]() ,2),点E坐标为(4,
,2),点E坐标为(4,![]() ),即可得CF=
),即可得CF=![]() ,BF=DF=2﹣
,BF=DF=2﹣![]() ,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值。
,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值。


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数表达式为y=x2-2x-3.
(1) 求b,c;
(2)求原函数图象的顶点坐标;
(3)求两个图象顶点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小山的东侧A点处有一个热气球,由于受西风的影响,以每分钟30米的速度沿与地面成60°角的方向飞行,20分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则A、B两点间的距离为________米.
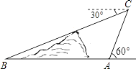
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn的面积为Sn,则Sn= .(用含n的式子表示)
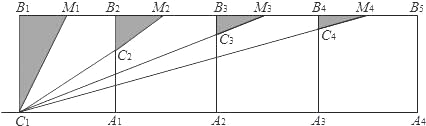
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com