
【题目】已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数表达式为y=x2-2x-3.
(1) 求b,c;
(2)求原函数图象的顶点坐标;
(3)求两个图象顶点之间的距离.
【答案】(1)2;0;(2)顶点坐标为(-1,-1);(3)原两个顶点之间的距离为![]() .
.
【解析】
先把平移后的函数化为顶点式表达,再根据二次函数的平移变化得出b、c的值,即可求出相应的顶点坐标即两顶点之间的距离.
(1)2;0
∵y=x2-2x-3= (x-1)2-4,
此函数经过向右平移2个单位长度,再向下平移3个单位长度得到,
故平移前的函数为y= (x+1)2-1,
y= (x+1)2-1=y=x2+2x,
故a=1,b=2;
(2)原函数的表达式为y= (x+1)2-1.
∴其图象的顶点坐标为(-1,-1).
(3)原图象的顶点为(-1,-1),新图象的顶点为(1,-4).
由勾股定理易得两个顶点之间的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
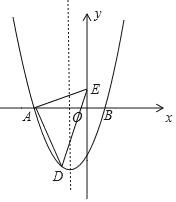
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为2,∠ABC=60°,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连结PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( )
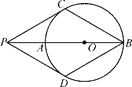
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
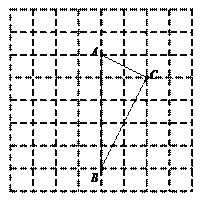
【题目】如图,在由边长为1的小正方形组成的网格图中,有一个格点三角形ABC.(注:顶点均在网格线交点处的三角形称为格点三角形.)
(1)△ABC是 三角形(填“锐角”、“直角”或“钝角”);
(2)若P、Q分别为线段AB、BC上的动点,当PC+PQ取得最小值时,
① 在网格中用无刻度的直尺,画出线段PC、PQ.(请保留作图痕迹.)
② 直接写出PC+PQ的最小值: .
查看答案和解析>>
科目:初中数学 来源: 题型:
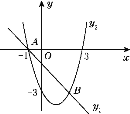
【题目】如图,A(-1,0),B(2,-3)两点在一次函数y=-x+m与二次函数y=ax2+bx-3的图象上.
(1)求m的值和二次函数的表达式;
(2)设二次函数的图象交y轴于点C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com