
【题目】如图①,正方形![]() 的边长为
的边长为![]() ,动点
,动点![]() 从点
从点![]() 出发,在正方形的边上沿
出发,在正方形的边上沿![]() 运动,设运动的时间为
运动,设运动的时间为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,
,![]() 与
与![]() 的函数图象如图②,请回答下列问题:
的函数图象如图②,请回答下列问题:

(1)点![]() 在
在![]() 上运动的时间为
上运动的时间为 ![]() ,在
,在![]() 上运动的速度为
上运动的速度为 ![]()
(2)设![]() 的面积为
的面积为![]() ,求当点
,求当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
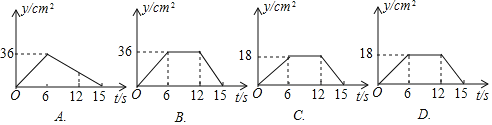
(3)①下列图表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是 .
之间的函数图象是 .
②当![]()
![]() 时,
时,![]() 的面积为
的面积为![]()
【答案】(1)6,2;(2)![]() ;(3)①C;②4或13.
;(3)①C;②4或13.
【解析】
(1)由图象得:点P在AB上运动的时间为6s,在CD上运动的速度为6÷(15-12)=2(cm/s);
(2)当点P在CD上运动时,由题意得:PC=2(t-12),得出PD=30-2t,由三角形面积公式即可得出答案;
(3)①当点P在AB上运动时,y与t之间的函数解析式为y=3t;当点P在BC上运动时,y与t之间的函数解析式为y=18;当点P在CD上运动时,y与t之间的函数解析式为y=-6t+90,即可得出答案;
②由题意分两种情况,即可得出结果.
(1)由题意得:点![]() 在
在![]() 上运动的时间为
上运动的时间为![]() ,
,
在![]() 上运动的速度为
上运动的速度为![]() ;
;
故答案为:6,2;
(2)当点![]() 在
在![]() 上运动时,
上运动时,
由题意得:![]() ,
,
![]() ,
,
![]() 的面积为
的面积为![]() ,
,
即![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ;
;
(3)①当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ;
;
当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ;
;
当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ,
,
![]() 表示
表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是
之间的函数图象是![]() ,
,
故答案为:![]() ;
;
②由题意得:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
即当![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
故答案为:4或13.


科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,本次上学途中,小明一共行驶了 米;
(2)小明在书店停留了 分钟,本次上学,小明一共用了 分钟;
(3)在整个上学的途中那个时间段小明骑车速度最快,最快的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=_____秒时,四边形ABPQ是直角梯形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】命题:如果两条平行线被第三条直线所截,那么一组内错角的平分线互相平行,如图为符合该命题的示意图.
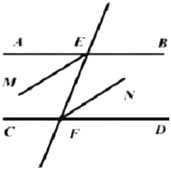
(1)请你根据图形把该命题用几何符号语言补充完整,己知:直线![]() 、
、![]() 被第三条直线
被第三条直线![]() 所截,且
所截,且![]() ,
,![]() 平分
平分![]() ,
,![]() 平分______,则______
平分______,则______![]() ______
______
(2)判断该命题的真假,若是假命题,请举例说明:若是真命题,请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB—BC的路径运动,到点C停止运动.过点E作 EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
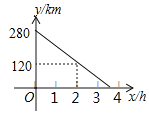
【题目】甲车从A地驶往B地,同时乙车从B地驶往A地,两车相向而行,匀速行驶,甲车距B地的距离y(km)与行驶时间x(h)之间的函数关系如图所示,乙车的速度是60km/h.
(1)求甲车的速度;
(2)当甲乙两车相遇后,乙车速度变为a(km/h),并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com