

分析 (1)如图1中,由AB为⊙O的直径,弦CD⊥AB,推出EC=ED,AC=AD,∠CAE=∠DAE,由FA=FP,推出∠FAP=∠FPA=∠DAB,即可证明MN∥AD.
(2)连接AM.由AD∥MN,推出$\widehat{AM}$=$\widehat{DN}$,推出AM=DN,由FM=DN,推出AM=FM,∠MAF=∠MFA,由MN∥AD,推出∠MFA=∠FAD,推出∠MAC=∠CDA,即可证明$\widehat{CM}$=$\widehat{CD}$.
(3)连接AG,作CT⊥AM交AM的延长线于T,CT交⊙O于R.由△AKG∽△CKB,可得AK•KB=CK•GK,设AK=x,KB=y,推出xy=30 ①,再证明△ACT≌△ACH,推出TC=CH=8AH=AT=$\sqrt{{x}^{2}-{3}^{2}}$,AC=$\sqrt{{x}^{2}-{3}^{2}+{8}^{2}}$,由CE2=AC2-AE2=KC2-KE2,推出x2-32+82-(x+$\frac{1}{2}$y)2=52-($\frac{1}{2}$y)2 ②,求出x、y,再根据TM•TA=TR•TC,想办法求出TA、TR、TC求出TM即可解决问题.
解答 (1)证明:如图1中,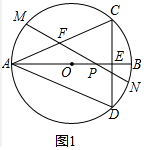
∵AB为⊙O的直径,弦CD⊥AB,
∴EC=ED,AC=AD,
∠CAE=∠DAE,
∵FA=FP,
∴∠FAP=∠FPA=∠DAB,
∴MN∥AD.
(2)解:连接AM.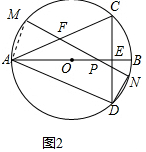
∵AD∥MN,
∴$\widehat{AM}$=$\widehat{DN}$,
∴AM=DN,
∵FM=DN,
∴AM=FM,
∴∠MAF=∠MFA,
∵MN∥AD,
∴∠MFA=∠FAD,
∴∠MAC=∠CDA,
∴$\widehat{CM}$=$\widehat{CD}$.
(3)连接AG,作CT⊥AM交AM的延长线于T,CT交⊙O于R.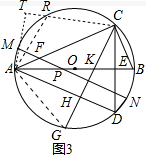
∵AD⊥CG,AB⊥CD,
∴∠AHK=∠CEK=90°,
∵∠AKH=∠CKE,
∴∠KAH=∠CKE=∠BCE,
∴∠ECK=∠ECB,
∵∠ECK+∠CKE=90°,∠ECB+∠CBE=90°,
∴∠CKE=∠CBE,
∴CK=CB=5,GK=CG-CK=6,
由△AKG∽△CKB,可得AK•KB=CK•GK,设AK=x,KB=y,
∴xy=30 ①,
∵∠GAH=∠GCD=∠BCD=∠DAK,易知∠G=∠AKG,
∴AG=AK,GH=HK=3,
∵∠CAM=∠CAD,
∴∠TCA=∠ACH,
∴AT=AH,∵AC=AC,
∴△ACT≌△ACH,
∴TC=CH=8AH=AT=$\sqrt{{x}^{2}-{3}^{2}}$,AC=$\sqrt{{x}^{2}-{3}^{2}+{8}^{2}}$,
∵CE2=AC2-AE2=KC2-KE2,
∴x2-32+82-(x+$\frac{1}{2}$y)2=52-($\frac{1}{2}$y)2 ②,
由①②可得x=3$\sqrt{5}$,y=2$\sqrt{5}$,
∴EC=$\sqrt{C{K}^{2}-K{E}^{2}}$=2$\sqrt{5}$,AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=10,AH=AT=$\sqrt{A{K}^{2}-H{K}^{2}}$=6,
∵∠ACR=∠ACG,
∴$\widehat{AR}$=$\widehat{AG}$,
∴AR=AG=AK=3$\sqrt{5}$,
∴RT=$\sqrt{A{R}^{2}-A{T}^{2}}$=3,
∵TM•TA=TR•TC,
∴TM•6=3•8,
∴TM=4.
∴AM=AT-TM=6-4=2,
∴DN=AM=2.
点评 本题考查圆综合题、垂径定理、相似三角形的判定和性质、全等三角形的判定和性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,学会构建方程组解决问题,属于中考压轴题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
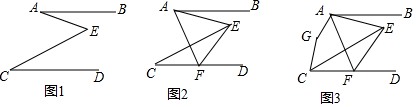
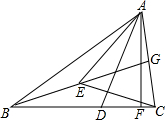 如图,在△ABC中,∠BAC=60°,∠ACB=80°,AD为∠BAC的角平分线,G、E分别是AC、BG的中点,AF⊥BC于F.求:
如图,在△ABC中,∠BAC=60°,∠ACB=80°,AD为∠BAC的角平分线,G、E分别是AC、BG的中点,AF⊥BC于F.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
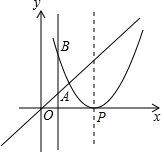 己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
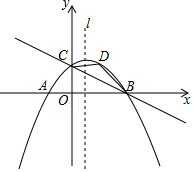 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与y轴交于点C(0,2),与x轴交于A,B两点,点A的坐标为(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与y轴交于点C(0,2),与x轴交于A,B两点,点A的坐标为(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
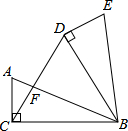 如图所示,在△ABC=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F.
如图所示,在△ABC=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com