
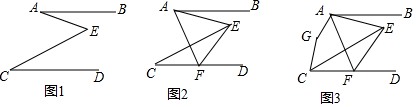
分析 (1)过E作EF∥AB,根据平行线的性质,即可得出∠A=∠AEF,∠C=∠CEF,进而得到∠AEC=∠AEF+∠CEF=∠A+∠C;
(2)设∠BAE=α,∠DCE=β,由(1)可得,∠AEC=∠BAE+∠C=α+β,根据角的和差关系可得,∠BAF=∠EAF+∠BAE=α+2β+α=2(α+β),最后根据∠AFC=∠BAF=2(α+β),可得∠AFC=2∠AEC;
(3)设∠G=α,根据5∠AFC=2∠G,可得∠AFC=$\frac{2}{5}$α,再根据∠AFC=2∠AEC,可得∠AEC=$\frac{1}{2}$∠AFC=$\frac{1}{5}$α,最后根据四边形AECG中,∠GCE与∠GAE互为补角,可得∠G+∠AEC=180°,据此可得方程α+$\frac{1}{5}$α=180°,求得∠G的度数为150°.
解答 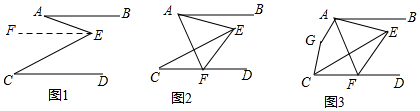 解:(1)如图,过E作EF∥AB,
解:(1)如图,过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠A+∠C;
(2)设∠BAE=α,∠DCE=β,则
由(1)可得,∠AEC=∠BAE+∠C=α+β,
∵∠EFD=2∠C,∠EFD=∠C+∠CEF,
∴∠C=∠CEF=β,
∴∠AEF=α+2β,
又∵∠FAE=∠FEA,
∴∠FAE=α+2β,
∴∠BAF=∠EAF+∠BAE=α+2β+α=2(α+β),
又∵AB∥CD,
∴∠AFC=∠BAF=2(α+β),
∴∠AFC=2∠AEC;
(3)设∠G=α,
根据5∠AFC=2∠G,可得∠AFC=$\frac{2}{5}$α,
又∵∠AFC=2∠AEC,
∴∠AEC=$\frac{1}{2}$∠AFC=$\frac{1}{5}$α,
∵四边形AECG中,∠GCE与∠GAE互为补角,
∴∠G+∠AEC=180°,
即α+$\frac{1}{5}$α=180°,
∴α=150°,
即∠G的度数为150°.
点评 本题主要考查了平行线的性质,三角形内角和定理以及四边形内角和的综合应用,解决问题的关键是掌握:两直线平行,内错角相等.解题时注意方程思想的运用.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
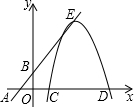 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
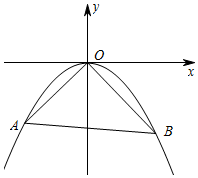 如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com