
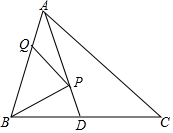
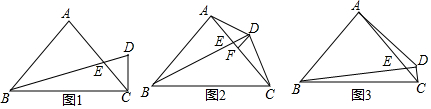
 已知:如图,△ABC中,点P,Q分别是∠BAC的平分线AD,边AB上的两个动点,∠C=α,BC=6.
已知:如图,△ABC中,点P,Q分别是∠BAC的平分线AD,边AB上的两个动点,∠C=α,BC=6.分析 (1)如图1,过B作BF⊥AC于F,过P作PQ⊥AB于Q,由AD是∠BAC的平分线.得出PQ=PF,这时PB+PQ有最小值,即BF的长度,运用勾股定理求出BF,即PB+PQ的最小值;
(2)如图2,同理可求得PB+PQ的最小值是6sin70°.
解答 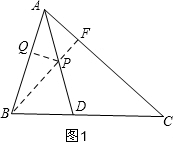 解:(1)如图1,过B作BF⊥AC于F,交AD于P,过P作PQ⊥AB于Q,
解:(1)如图1,过B作BF⊥AC于F,交AD于P,过P作PQ⊥AB于Q,
∵AD平分∠BAC,
∴PF=PQ,此时PB+PQ为最小,即为BF的长,
∵∠BFC=90°,∠ACB=α=45°,
∴BF=FC,
∵BC=6,
∴BF2+FC2=BC2,
∴BF=$±3\sqrt{2}$,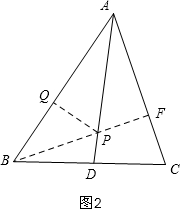
∴PB+PQ的最小值为3$\sqrt{2}$;
(2)如图2,过F作BF⊥AC于F,过P作PQ⊥AB于Q,
同理可知:BF=PB+PQ,且此时BF就是PB+PQ的最小值;
在Rt△BFC中,sin70°=$\frac{BE}{BC}$
∴BE=BC•sin70°=6sin70°
即PB+PQ的最小值是6sin70°.
点评 本题主要考查了轴对称--最短路径问题,解题的关键是找出满足PC+PQ有最小值时点P和Q的位置.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:填空题
 如图,七年级(1)班的学生为节约资源将数学课上正方体展开的图形上写上“放飞我的梦想”,作为班会课横幅,若把这个纸片再折叠成正方体,那么与“放”相对面上的字是梦.
如图,七年级(1)班的学生为节约资源将数学课上正方体展开的图形上写上“放飞我的梦想”,作为班会课横幅,若把这个纸片再折叠成正方体,那么与“放”相对面上的字是梦.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com