
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am-b).
其中所有正确的结论是( )
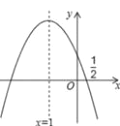
A. ①②③ B. ①③④ C. ①②③⑤ D. ①③⑤
【答案】D
【解析】试题分析:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+4c=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(﹣![]() ,0),
,0),
当x=﹣![]() 时,y=0,即a(﹣
时,y=0,即a(﹣![]() )2+b×(﹣
)2+b×(﹣![]() )+c=0,
)+c=0,
整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,
∴a﹣b+c>m2a﹣mb+c(m≠1),
∴a﹣b>m(am﹣b),所以⑤正确;
故选D.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
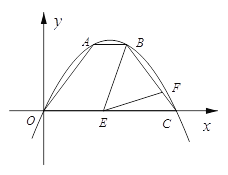
【题目】如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.
(1)求抛物线的解析式;
(2)若四边形OABE的面积为14,求S△ECF;
(3)是否存在点E,使得△BEF为等腰三角形?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
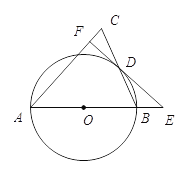
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.
(1)求证:EF⊥AC;
(2)若AF=9,EF=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天的运营全是在东西走向的人民大街进行的,如果规定向东为正,向西为负,他这天下午的行车里程如下(单位:km)
+10、-3、-8、+11、-10、+12、+4、-15、-16、+15
(1)将最后一名乘客送到目的地时,小李距下午出车地点的距离是多少?
(2)若汽车的耗油量为0.5L/㎞,那么这天下午汽车共耗油多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com