莲花山公园管理处计划购买甲、乙两种花木共6000株，甲种花木每株0.5元，乙种花木每株0.8元．相关资料表明：甲、乙两种花木的成活率分别为90%和95%．
（1）若购买这批花木共用了3600元，求甲、乙两种花木各购买了多少株？
（2）若要使这批花木的成活率不低于93%，且购买花木的总费用最低，应如何选购花木？
科目：初中数学 来源： 题型：
已知：A=2a2+3ab﹣2a﹣1，B=﹣a2+ab+1
（1）当a=﹣1，b=2时，求4A﹣（3A﹣2B）的值；
（2）若（1）中的代数式的值与a的取值无关，求b的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
商场经销甲、乙两种商品，甲种商品每件进价15元，售价20元；乙种商品每件进价35元，售价45元．
（1）若该商场同时购进甲、乙两种商品共100件恰好用去2700元，求能购进甲、乙两种商品各多少件？
（2）该商场为使甲、乙两种商品共100件的总利润（利润＝售价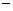
进价）不少于750元，且不超过760元，请你帮助该商场设计相应的进货方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
古希腊著名的毕达哥拉斯学派把1、3、6、10 …，这样的数称为“三角形数”，而把1、4、9、16…，这样的数称为“正方形数”．
（1）第5个三角形数是 ，第n个“三角形数”是 ，第5个“正方形数”是 ，第n个正方形数是 ；
（2）经探究我们发现：任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．
例如：①4=1+3，②9=3+6，③16=6+10，④ ，⑤ ，…．
请写出上面第4个和第5个等式；
（3）在（2）中，请探究第n个等式，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
某班将举行“庆祝建党90周年知识竞赛“活动，班长安排小明购买奖品，下面两图是小明买回奖品时与班长的对话情境：
请根据上面的信息．解决问題：
（1）试计算两种笔记本各买了多少本？
（2）请你解释：小明为什么不可能找回68元？
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：如图，如果∠A=∠F，∠C=∠D，那么∠BMN与∠CNM互补﹒
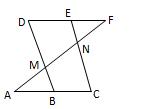
证明：因为∠A=∠F（已知）
所以 ∥ （ ）
所以∠D=∠ （ ）
又因为∠C=∠D（已知）
所以∠C=∠ （ ）
所以 ∥ （ ）
所以∠BMN与∠CNM互补.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
株，乙种花木
株，
.
.
时，总费用最低.
、b的形式，则a2014+b2015的值__________．
与点N
关于
轴对称，则
．