已知：如图，如果∠A=∠F，∠C=∠D，那么∠BMN与∠CNM互补﹒
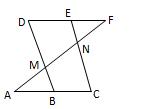
证明：因为∠A=∠F（已知）
所以 ∥ （ ）
所以∠D=∠ （ ）
又因为∠C=∠D（已知）
所以∠C=∠ （ ）
所以 ∥ （ ）
所以∠BMN与∠CNM互补.
科目：初中数学 来源： 题型：
在计算3+5+7+9+11+13的值时，小明直接计算出结果为48，爱动脑筋的小红，发现这6
个数据的特点后，用
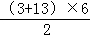的方法来计算，也得出同样的结果．
请用上面小红的发现解答下面问题：
某公司对外出租一商铺，符合条件的两商户A、B分别拟定上缴利润方案如下：
A：每年结算一次上缴房租，第一年上缴1.5万元，以后每年比前一年增加1万元；
B：每半年结算一次上缴房租，第一个半年上缴0.3万元，以后每半年比前半年增加0.3万元；
（1）如果承租期限3年，则A商户上缴房租的总金额为__________万元，B商户上缴房租的总金额为__________万元；
（2）如果承租期限为n年，分别求A、B两商户上缴房租的总金额；（用含n的代数式表示）
（3）如果承租期限n=20时，那么哪个商户上缴房租的总金额比较多？
查看答案和解析>>
科目：初中数学 来源： 题型：
一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为3＋（－2
）＝1．
若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}＋{c，d}＝{a＋c，b＋d}．
解决问题：
（1）计算：{3，1}＋{1，2}；{1，2}＋{3，1}；
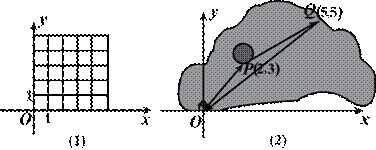
（2）动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”{3，1}平移，最后的位置还是点B吗？在图（1）中画出四边形OABC；
（3）如图（2），一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O．请用“平移量”加法算式表示它的航行过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
莲花山公园管理处计划购买甲、乙两种花木共6000株，甲种花木每株0.5元，乙种花木每株0.8元．相关资料表明：甲、乙两种花木的成活率分别为90%和95%．
（1）若购买这批花木共用了3600元，求甲、乙两种花木各购买了多少株？
（2）若要使这批花木的成活率不低于93%，且购买花木的总费用最低，应如何选购花木？
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，已知AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E．∠ADC =70°．
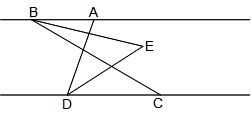
（1）求∠EDC的度数；
（2）若∠ABC =n°，求∠BED的度数（用含n的代数式表示）；
（3）将线段BC沿DC方向平移， 使得点B在点A的右侧，其他条件不变，画出图形并判断∠BED的度数是否改变，若改变，求出它的度数（用含n的式子表示），不改变，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在ΔABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
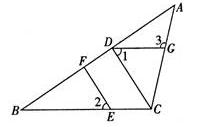
（1）CD与EF平行吗？为什么？
（2）如果∠1=∠2，且∠3=115°，求∠ACB的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，求x＋y的值．
