
如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
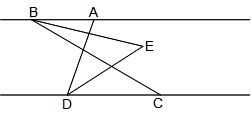
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
解:(1)∵DE平分∠ADC,∠ADC=70°,∴∠EDC= ∠ADC=
∠ADC= ×70°=35°;
×70°=35°;
(2)过点E作EF∥AB,

∵AB∥CD, ∴AB∥CD∥EF, ∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠A BE=
BE= ∠ABC=
∠ABC= n°,∠CDE=
n°,∠CDE= ∠ADC=35°, ∴∠BED=∠BEF+∠DEF=
∠ADC=35°, ∴∠BED=∠BEF+∠DEF= n°+35°;
n°+35°;
(3)过点E作EF∥AB
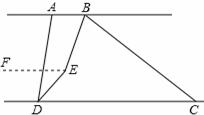
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70° ∴∠ABE= ∠ABC=
∠ABC= n°,∠CDE=
n°,∠CDE= ∠ADC=35°
∠ADC=35°
∵AB∥CD,∴AB∥CD∥EF, ∴∠BEF=180°-∠ABE=180°- n°,∠CDE=∠DEF=35°,
n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°- n°+35°=215°-
n°+35°=215°- n°.
n°.
故∠BED的度数发生了改为,改变为(215- n)°.
n)°.
【难度】困难


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
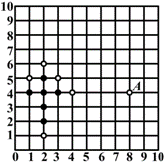
五子棋深受广大棋友的喜爱.规则是:10×10的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上首先连成五颗者为胜.如图是小张和小王的对弈图(小张执黑子先行,小王执白子后走).
观察棋盘思考:若A点的位置记作(8,4),小张必须在哪个位置上落子才不会让小王在短时间内获胜?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
古希腊著名的毕达哥拉斯学派把1、3、6、10 …,这样的数称为“三角形数”,而把1、4、9、16…,这样的数称为“正方形数”.
(1)第5个三角形数是 ,第n个“三角形数”是 ,第5个“正方形数”是 ,第n个正方形数是 ;
(2)经探究我们发现:任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.
例如:①4=1+3,②9=3+6,③16=6+10,④ ,⑤ ,….
请写出上面第4个和第5个等式;
(3)在(2)中,请探究第n个等式,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数S(次/分)与这个人年龄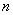 (岁)满足关系式:
(岁)满足关系式: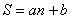 ,其中
,其中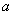 、
、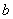 均为常数.
均为常数.
(1)根据下图中提供的信息,求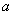 、
、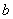 的值;
的值;
(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,如果∠A=∠F,∠C=∠D,那么∠BMN与∠CNM互补﹒
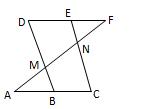
证明:因为∠A=∠F(已知)
所以 ∥ ( )
所以∠D=∠ ( )
又因为∠C=∠D(已知)
所以∠C=∠ ( )
所以 ∥ ( )
所以∠BMN与∠CNM互补.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com