
分析 (1)根据求根公式计算可得;
(2)把x=m代入方程得:m2+m-1=0,即m2+m=1,再整体代入原式=m2+2m+1+m2-1=2(m2+m)可得.
解答 解:(1)∵a=3,b=-2$\sqrt{3}$,c=1,
∴△=12-4×3×1=0,
方程有两个相等的实数根x1=x2=-$\frac{-2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$;
(2)把x=m代入方程得:m2+m-1=0,即m2+m=1,
则原式=m2+2m+1+m2-1=2(m2+m)=2.
点评 本题主要考查解一元二次方程和方程的解的定义,熟练掌握解一元二次方程的几种方法和方程的解得定义是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
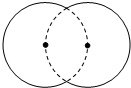 如图,图中实线部分是半径为9m的两条等弧组成的花坛,若每条弧所在的圆都经过另一个圆的圆心,则这个花坛的周长为( )
如图,图中实线部分是半径为9m的两条等弧组成的花坛,若每条弧所在的圆都经过另一个圆的圆心,则这个花坛的周长为( )| A. | 12π m | B. | 18π m | C. | 20π m | D. | 24π m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com