
【题目】已知:如图,△ABC中,AD⊥BC,AB=AE,点E在AC的垂直平分线上.
(1)请问:AB、BD、DC有何数量关系;并说明理由.
(2)如果∠B=60°,证明:CD=3BD.

【答案】(1)AB+BD=CD;理由见解析;(2)证明见解析.
【解析】
(1)由AD⊥BC,BD=DE,点E在AC的垂直平分线上,根据线段垂直平分线的性质,可得AE=EC,AB=AE,继而证得AB+BD=AE+DE=DC.
(2)易得△ABE是等边三角形,则可得△ABC是直角三角形,且∠BAD=∠C=30°,然后由含30°角的直角三角形的性质,证得结论.
解:(1)AB+BD=DC.理由如下:
∵AD⊥BC,BD=DE,∴AB=AE,BD=DE,
∵点E在AC的垂直平分线上,∴AE=CE,
∴AB+BD=AE+DE=DC.
(2)∵AB=AE,∠B=60°,∴△ABE是等边三角形,∴∠AEB=∠B=∠BAE=60°,
∵AE=EC,∴∠C=∠CAE=![]() ∠AEB=30°,∴∠BAC=90°,∠BAD=30°,
∠AEB=30°,∴∠BAC=90°,∠BAD=30°,
在Rt△ABC中,BC=2AB,在Rt△AABD中,AB=2BD,
∴BC=4BD,
∴DC=3BD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给人们的生活带来方便,2017年兴化市准备在部分城区实施公共自行车免费服务.图1是公共自行车的实物图,图2是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=35cm,DF=24cm,AF=30cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离(结果保留整数).
(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )

A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数是选择科目B的人数的两倍
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
查看答案和解析>>
科目:初中数学 来源: 题型:
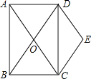
【题目】如图,矩形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 关于
关于![]() 的对称图形为
的对称图形为![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
①根据题意补全图形;
②若![]() =
=![]() ,请用等式表示线段
,请用等式表示线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b满足,![]() 且A(a,0)、B(0,b)
且A(a,0)、B(0,b)

(1) 如图,在x正半轴上有一点C(x,0).若△ABC的面积大于6,请直接写出x的取值范围____________;
(2)若在平面直角坐标系第四象限上存在一点N,N的坐标为(n,﹣n),满足4≤S△ABN≤8,求n的取值范围.
(3)若在平面直角坐标系上存在一点M,M的坐标为(m,﹣2m),请通过计算说明:无论m取何值△ABM的面积为定值,并求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com