
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D为BC中点,点E在边AB上,连接DE,过点D作DF⊥DE交AC于点F.连接EF.下列结论:①BE+CF=![]() BC;②AD≥EF;③S四边形AEDF=
BC;②AD≥EF;③S四边形AEDF=![]() AD2;④S△AEF≤
AD2;④S△AEF≤![]() ,其中正确的是_____(填写所有正确结论的序号).
,其中正确的是_____(填写所有正确结论的序号).
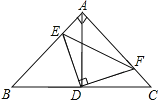
【答案】①③④.
【解析】
由“ASA”可证△ADE≌△CDF,可得AE=CF,S△ADE=S△CDF,由等腰直角三角形的性质可判断①,③,由三角形的三边关系可判断②,由三角形面积关系可判断④.
解:∵AB=AC,∠BAC=90°,点D为BC中点,
∴BD=CD=AD=![]() BC,∠BAD=∠CAD=∠C=45°,AD⊥BC,BC=
BC,∠BAD=∠CAD=∠C=45°,AD⊥BC,BC=![]() AB,
AB,
∵DF⊥DE,
∴∠EDF=∠ADC=90°,
∴∠ADE=∠CDF,且AD=CD,∠BAD=∠C,
∴△ADE≌△CDF(ASA),
∴AE=CF,
∴BE+CF=BE+AE=AB,且BC=![]() AB,
AB,
∴BE+CF=![]() BC,故①正确;
BC,故①正确;
∵AE+AF≥EF,
∴AF+CF≥EF,
∴AC≥EF,
∴![]() AD≥EF,故②错误;
AD≥EF,故②错误;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四边形AEDF=S△ADF+S△CDF=S△ADC=![]() ×AD2,故③正确;
×AD2,故③正确;
∵S△AEF=![]() ×AE×AF,且AE+AF=AC,
×AE×AF,且AE+AF=AC,
∴当AE=AF时,S△AEF的最大值=![]() S△ABC,
S△ABC,
∴S△AEF≤![]() ,故④正确,
,故④正确,
故答案为:① ③ ④


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB—BC的路径运动,到点C停止运动.过点E作 EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下图:
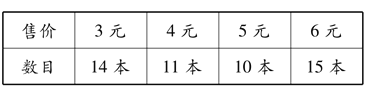
下列说法正确的是( )
A.该班级所售图书的总数收入是226元
B.在该班级所售图书价格组成的一组数据中,中位数是4
C.在该班级所售图书价格组成的一组数据中,众数是15
D.在该班级所售图书价格组成的一组数据中,方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
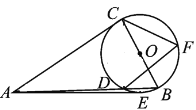
【题目】如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上的两点,连结AE、CF、DF,满足EA=CA.
(1)求证:AE是⊙O的切线;
(2)若⊙O的半径是3,tan∠CFD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A在y轴上,点B、C在x轴上;OA、OB长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB,BC=6;
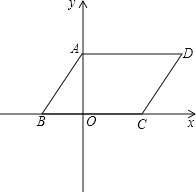
(1)写出点D的坐标 ;
(2)若点E为x轴上一点,且S△AOE=![]() ,
,
①求点E的坐标;
②判断△AOE与△AOD是否相似并说明理由;
(3)若点M是坐标系内一点,在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52°,BC=5米,CD=35米,DE=19米,则铁塔AB的高度约为(参考数据:sin52°≈0.79,tan52°≈1.28)( )

A.28米B.29.6米C.36.6米D.57.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
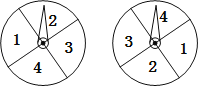
【题目】学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com