练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若关于x的一元二次方程有实根．

    （1）求k的取值范围；

    （2）当k取得最大整数值时，求此时方程的根．


    解：(1) ∵ 关于x的一元二次方程有实根，

    ∴                                                  

    且 ，

    解得

    ∴ k的取值范围是，且．                      

    (2) 在，且的范围内，最大整数k为1．                

    此时，方程化为．

    ∴ 方程的根为，．                                 


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列计算正确的是（   ）

       A．       B． 

       C．   D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D，C´的位置，若∠EFB=65°，则∠AED´等于           °.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差：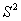

    甲

    乙

    丙

    丁

    平均数x（cm）

    175

    173

    175

    174

    方差（cm2）

    3.5

    3.5

    12.5

    15

    根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择

    A．甲               B．乙                   C．丙        D．丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


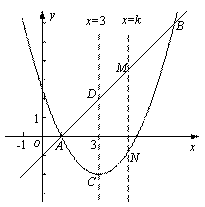
    已知抛物线的顶点为点C．

    （1）求证：不论m为何实数，该抛物线与x轴总有两个不同的交点；

    （2）若抛物线的对称轴为直线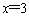，求m的值和C点坐标；

    （3）如图，直线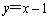与（2）中的抛物线交于A、B两点，并与它的对称轴交于点D．直线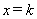交直线AB于点M，交抛物线于点N．求当k为何值时，以C，D，M，N为顶点的四边形是平行四边形．



    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算中正确的是（　　）

    A．　　  B．　          C．　      D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


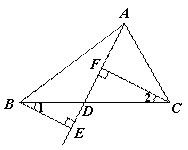
    完成下面的证明．

    已知：如图， D是BC上任意一点，BE⊥AD，交AD的

    延长线于点E，CF⊥AD，垂足为F． 

    求证：∠1＝∠2．

    证明：∵BE⊥AD ，                                               

    ∴∠BED＝         °（                     ）．

    ∵CF⊥AD，

    ∴∠CFD＝         °．

    ∴∠BED＝∠CFD．

    ∴BE∥CF（                                    ）．

    ∴∠1＝∠2（                                   ）．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，∠ACB=90° ，点O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D，E，F分别为垂足，且AB=10，BC=8，则点O到三边AB,AC,BC的距离分别是（   ）

    A.2，2，2    B.3，3，3   C.4，4，4   D.2，3，5

    查看答案和解析>>

    同步练习册答案