
已知抛物线 的顶点为点C.
的顶点为点C.
(1)求证:不论m为何实数,该抛物线与x轴总有两个不同的交点;
(2)若抛物线的对称轴为直线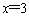 ,求m的值和C点坐标;
,求m的值和C点坐标;
(3)如图,直线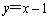 与(2)中的抛物线交于A、B两点,并与它的对称轴交于点D.直线
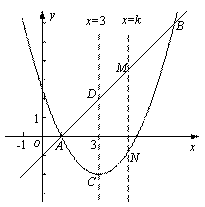
与(2)中的抛物线交于A、B两点,并与它的对称轴交于点D.直线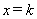 交直线AB于点M,交抛物线于点N.求当k为何值时,以C,D,M,N为顶点的四边形是平行四边形.
交直线AB于点M,交抛物线于点N.求当k为何值时,以C,D,M,N为顶点的四边形是平行四边形.

(1)Δ=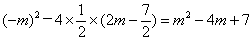
=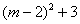 .
.
∵不论m为何实数,总有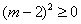 ,∴Δ=
,∴Δ=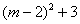 >0,
>0,
∴无论m为何实数,方程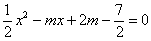 总有两个不相等的实数根,
总有两个不相等的实数根,
∴无论m为何实数,抛物线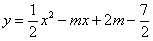 与x轴总有两个不同的交点.
与x轴总有两个不同的交点.
(2)∵ 抛物线的对称轴为直线x=3,
∴ 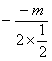 =3,即m=3,
=3,即m=3,
此时,抛物线的解析式为y=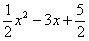 =
=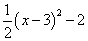 ,
,
∴顶点C坐标为(3,-2).
(3) ∵CD∥MN,C,D,M,N为顶点的四边形是平行四边形,
∴四边形CDMN是平行四边形或四边形CDNM是平行四边形.
由已知D(3,2),M(k,k-1),N(k, ),
),
∵C(3,-2),∴ CD=4.
∴MN=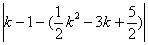 =CD=4.
=CD=4.
①当四边形CDMN是平行四边形,
MN=k-1-( )=4,
)=4,
整理得 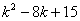 =0,
=0,
解得 k1=3(不合题意,舍去),k2=5.
②当四边形CDNM是平行四边形,
NM= -(k-1)=4,
-(k-1)=4,
整理得 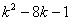 =0,
=0,
解得 k3=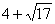 ,k4=
,k4=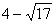 .
.
综上所述,k=5,或k=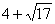 ,或k=
,或k=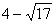 时,可使得C、D、M、N为顶点的四边形是平行四边形.
时,可使得C、D、M、N为顶点的四边形是平行四边形.


科目:初中数学 来源: 题型:
学生课业负担问题越来越受到社会的关注.为此某媒体记者随机调查了某区县若干名中学生家长对“留作业”的态度(态度分为:A:赞成多留作业; B:认为教师留作业量要适当;C:无所谓,尊重学校的安排),并将调査结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调査中,共调査了 名中学生家长;
(2)将图1补充完整;
(3)根据抽样调查结果,请你估计该区县8 000名中学生家长中有多少名家长持无所谓态度?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com