
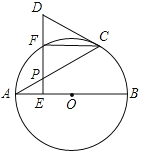
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.
(1)求证:DC=DP;
(2)若∠CAB=30°,当F是![]() 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
【答案】(1)证明见解析;(2)以A,O,C,F为顶点的四边形是菱形.
【解析】
试题分析:(1)连接BC、OC,利用圆周角定理和切线的性质可得∠B=∠ACD,由PE⊥AB,易得∠APE=∠DPC=∠B,等量代换可得∠DPC=∠ACD,可证得结论;
(2)由∠CAB=30°易得△OBC为等边三角形,可得∠AOC=120°,由F是![]() 的中点,易得△AOF与△COF均为等边三角形,可得AF=AO=OC=CF,易得以A,O,C,F为顶点的四边形是菱形.
的中点,易得△AOF与△COF均为等边三角形,可得AF=AO=OC=CF,易得以A,O,C,F为顶点的四边形是菱形.
试题解析:(1)连接BC、OC,∵AB是⊙O的直径,∴∠OCD=90°,∴∠OCA+∠OCB=90°,∵∠OCA=∠OAC,∠B=∠OCB,∴∠OAC+∠B=90°,∵CD为切线,∴∠OCD=90°,∴∠OCA+∠ACD=90°,∴∠B=∠ACD,∵PE⊥AB,∴∠APE=∠DPC=∠B,∴∠DPC=∠ACD,∴AP=DC;
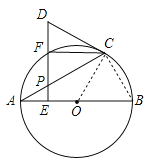
(2)以A,O,C,F为顶点的四边形是菱形.理由如下:
∵∠CAB=30°,∴∠B=60°,∴△OBC为等边三角形,∴∠AOC=120°,连接OF,AF,∵F是![]() 的中点,∴∠AOF=∠COF=60°,∴△AOF与△COF均为等边三角形,∴AF=AO=OC=CF,∴四边形OACF为菱形.
的中点,∴∠AOF=∠COF=60°,∴△AOF与△COF均为等边三角形,∴AF=AO=OC=CF,∴四边形OACF为菱形.



 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(﹣1,3)、B(﹣4,1)、C(﹣2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1 , 再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2 . 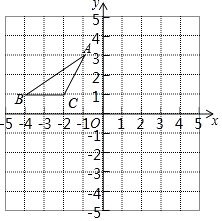
(1)分别作出△A1B1C1和△A2B2C2;
(2)求△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
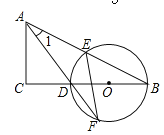
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=
,EF=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 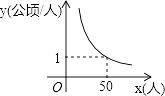
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级三位老师带部分学生去红色旅游,联系了甲、乙两家旅行社,甲旅行社说:“老师免费,学生打八折。”乙旅行社说:“包括老师在内全部打七折.”若全程费用为每人200元,求:
(1)设有 x 名学生参加活动,请分别写出参加两家旅行社的费用的代数式;
(2)若有25名学生参加活动,问选择哪家旅行社更合算?
(3)分别计算21名和15名学生参加活动时两家旅行社的费用?根据上面的结果应如何选择哪家旅行社更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A﹣空气污染,B﹣淡水资源危机,C﹣土地荒漠化,D﹣全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:
关注问题 | 频数 | 频率 |
A | 24 | b |
B | 12 | 0.2 |
C | n | 0.1 |
D | 18 | m |
合计 | a | 1 |

根据表中提供的信息解答以下问题:
(1)表中的a= , b= .
(2)请将条形统计图补充完整;
(3)如果凯文所在的学校有3600名学生,那么根据凯文提供的信息估计该校关注“全球变暖”的学生大约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
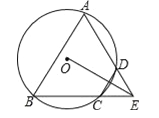
【题目】如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)求证:∠A=∠AEB;
(2)如果DC⊥OE,求证:△ABE是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com