
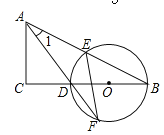
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=
,EF=![]() ,求CD的长.
,求CD的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连接DE,由BD是⊙O的直径,得到∠DEB=90°,由于E是AB的中点,得到DA=DB,根据等腰三角形的性质得到∠1=∠B等量代换即可得到结论;
(2)g根据等腰三角形的判定定理得到AE=EF=![]() ,推出AB=2AE=
,推出AB=2AE=![]() ,在Rt△ABC中,根据勾股定理得到BC=8,设CD=x,则AD=BD=8﹣x,根据勾股定理列方程即可得到结论.
,在Rt△ABC中,根据勾股定理得到BC=8,设CD=x,则AD=BD=8﹣x,根据勾股定理列方程即可得到结论.
试题解析:(1)证明:连接DE,∵BD是⊙O的直径,∴∠DEB=90°,∵E是AB的中点,∴DA=DB,∴∠1=∠B,∵∠B=∠F,∴∠1=∠F;
(2)∵∠1=∠F,∴AE=EF=![]() ,∴AB=2AE=
,∴AB=2AE=![]() ,在Rt△ABC中,AC=ABsinB=4,∴BC=
,在Rt△ABC中,AC=ABsinB=4,∴BC=![]() =8,设CD=x,则AD=BD=8﹣x,∵
=8,设CD=x,则AD=BD=8﹣x,∵![]() ,即
,即![]() ,∴x=3,即CD=3.
,∴x=3,即CD=3.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,
交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.

(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数![]() 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若此方程的一个根是1,请求出方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
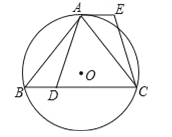
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t. 
(1)求证:在运动过程中,不管t取何值,都有S△AED=2S△DGC .
(2)当t取何值时,△DFE与△DMG全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com