
【题目】如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t. 
(1)求证:在运动过程中,不管t取何值,都有S△AED=2S△DGC .
(2)当t取何值时,△DFE与△DMG全等.
【答案】
(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
∵S△AED= ![]() AEDF,S△DGC=
AEDF,S△DGC= ![]() CGDM,
CGDM,
∴ ![]() =
= ![]() ,
,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴ ![]() =2,
=2,
即 ![]() =2,
=2,
∴在运动过程中,不管取何值,都有S△AED=2S△DGC
(2)解:设时间为t时,△DFE与△DMG全等,则EF=MG,
①当M在线段CG的延长线上时,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴EF=AF﹣AE=10﹣2t,MG=AC﹣CG﹣AM=4﹣t,
即10﹣2t=4﹣t,
解得:t=6,
当t=6时,MG=﹣2,所以舍去;
②当M在线段CG上时,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴EF=AF﹣AE=10﹣2t,MG=AM﹣(AC﹣CG)=t﹣4,
即10﹣2t=t﹣4,
解得:t= ![]() ,
,
综上所述当t= ![]() 时,△DFE与△DMG全等
时,△DFE与△DMG全等
【解析】(1)由角平分线的性质可知DF=DM,所以△AED和△DEG的面积转化为底AE和CG的比值,根据路程=速度×时间求出AE和CG的长度即可证明在运动过程中,不管取何值,都有S△AED=2S△DGC . (2)若△DFE与△DMG全等,则EF=MG,利用已知条件求出EF和MG的长度,建立方程解方程即可求出运动的时间.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
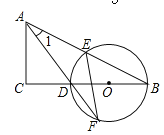
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=
,EF=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
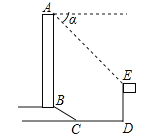
A.30.6 B.32.1 C.37.9 D.39.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣6x﹣8=0,下列变形正确的是( )
A. (x﹣6)2=﹣8+36 B. (x﹣6)2=8+36 C. (x﹣3)2=8+9 D. (x﹣3)2=﹣8+9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面图形上的任意两点P,Q,如果经过某种变换(如:平移、旋转、轴对称等)得到新图形上的对应点P′,Q′,保持P P′= Q Q′,我们把这种对应点连线相等的变换称为“同步变换”。对于三种变换: ①平移、②旋转、③轴对称,其中一定是“同步变换”的有(填序号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30°
C.∠ADE=![]() ∠ADC D.∠ADE=
∠ADC D.∠ADE=![]() ∠ADC
∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
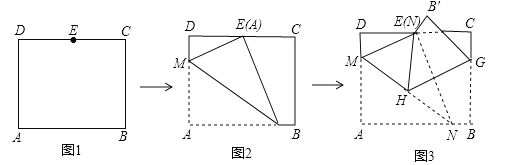
【题目】如图1,在矩形纸片ABCD中,AB=![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME/NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME/NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com